Quantifying quantumness: A mathematical project 'of immense beauty'

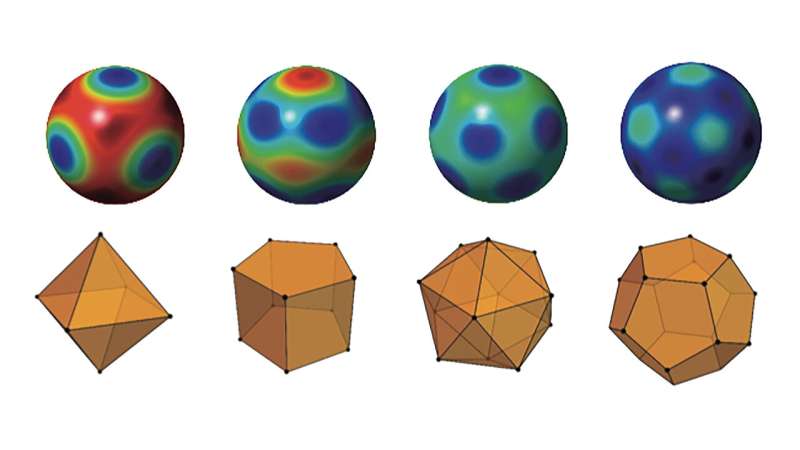
Large objects, such as baseballs, vehicles, and planets, behave in accordance with the classical laws of mechanics formulated by Sir Isaac Newton. Small ones, such as atoms and subatomic particles, are governed by quantum mechanics, where an object can behave as both a wave and a particle.

The boundary between the classical and quantum realms has always been of great interest. Research reported in AVS Quantum Science, considers the question of what makes something "more quantum" than another—is there a way to characterize "quantumness"? The authors report they have found a way to do just that.

The degree of quantumness is important for applications such as quantum computing and quantum sensing, which offer advantages that are not found in their classical counterparts. Understanding these advantages requires, in turn, an understanding of the degree of quantumness of the physical systems involved.

Rather than proposing a scale whose values would be associated with the degree of quantumness, the authors of this study look at extrema, namely those states that are either the most quantum or the least quantum. Author Luis Sanchez-Soto said the idea for the study came from a question posed at a scientific meeting.

"I was giving a seminar on this topic when someone asked me the question: 'You guys in quantum optics always talk about the most classical states, but what about the most quantum states?'" he said.

It has long been understood that so-called coherent states can be described as quasi-classical. Coherent states occur, for example, in a laser, where light from multiple photon sources are in phase making them the least quantum of states.

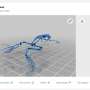
A quantum system can often be represented mathematically by points on a sphere. This type of representation is called a Majorana constellation, and for coherent states, the constellation is simply a single point. Since these are the least quantum of states, the most quantum ones would have constellations that cover more of the sphere.

The investigators looked at several ways that other scientists have explored quantumness and considered the Majorana constellation for each way. They then asked what the most evenly distributed set of points on a sphere for this approach is.

As Sanchez-Soto and his colleagues considered the question of quantumness, they realized it was a mathematical project "of immense beauty," in addition to being useful.