Research team discovers uniquely quantum effect in erasing information
Researchers from Trinity have discovered a uniquely quantum effect in erasing information that may have significant implications for the design of quantum computing chips. Their surprising discovery brings back to life the paradoxical "Maxwell's demon," which has tormented physicists for over 150 years.
The thermodynamics of computation was brought to the fore in 1961 when Rolf Landauer, then at IBM, discovered a relationship between the dissipation of heat and logically irreversible operations. Landauer is known for the mantra "Information is Physical," which reminds us that information is not abstract and is encoded on physical hardware.
The "bit" is the currency of information (it can be either zero or one) and Landauer discovered that when a bit is erased there is a minimum amount of heat released. This is known as Landauer's bound and is the definitive link between information theory and thermodynamics.
Professor John Goold's QuSys group at Trinity is analyzing this topic with quantum computing in mind, where a quantum bit (a qubit, which can be zero and one at the same time) is erased.
In just-published work in the journal, Physical Review Letters, the group discovered that the quantum nature of the information to be erased can lead to large deviations in the heat dissipation, which is not present in conventional bit erasure.
Thermodynamics and Maxwell's demon
One hundred years previous to Landauer's discovery people like Viennese scientist, Ludwig Boltzmann, and Scottish physicist, James Clerk Maxwell, were formulating the kinetic theory of gases, reviving an old idea of the ancient Greeks by thinking about matter being made of atoms and deriving macroscopic thermodynamics from microscopic dynamics.
Professor Goold says: "Statistical mechanics tells us that things like pressure and temperature, and even the laws of thermodynamics themselves, can be understood by the average behavior of the atomic constituents of matter. The second law of thermodynamics concerns something called entropy which, in a nutshell, is a measure of the disorder in a process. The second law tells us that in the absence of external intervention, all processes in the universe tend, on average, to increase their entropy and reach a state known as thermal equilibrium.
"It tells us that, when mixed, two gases at different temperatures will reach a new state of equilibrium at the average temperature of the two. It is the ultimate law in the sense that every dynamical system is subject to it. There is no escape: all things will reach equilibrium, even you."
However, the founding fathers of statistical mechanics were trying to pick holes in the second law right from the beginning of the kinetic theory. Consider again the example of a gas in equilibrium: Maxwell imagined a hypothetical "neat-fingered" being with the ability to track and sort particles in a gas based on their speed.
Maxwell's demon, as the being became known, could quickly open and shut a trap door in a box containing a gas, and let hot particles through to one side of the box but restrict cold ones to the other. This scenario seems to contradict the second law of thermodynamics as the overall entropy appears to decrease and perhaps physics' most famous paradox was born.
But what about Landauer's discovery about the heat-dissipated cost of erasing information? Well, it took another 20 years until that was fully appreciated, the paradox solved, and Maxwell's demon finally exorcised.
Landauer's work inspired Charlie Bennett—also at IBM—to investigate the idea of reversible computing. In one982 Bennett argued that the demon must have a memory, and that it is not the measurement but the erasure of the information in the demon's memory which is the act that restores the second law in the paradox. And, as a result, computation thermodynamics was born.
New findings
Now, 40 years on, this is where the new work led by Professor Goold's group comes to the fore, with the spotlight on quantum computation thermodynamics.
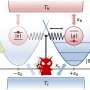
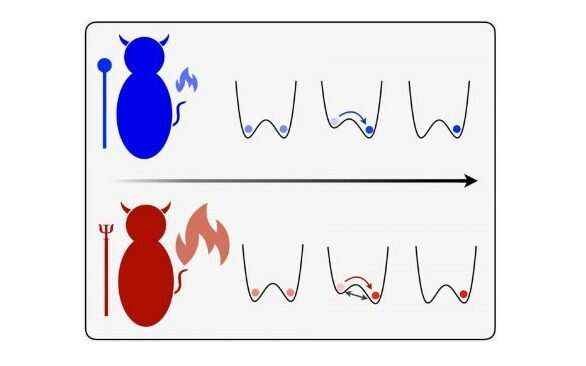
In the recent paper, published with collaborator Harry Miller at the University of Manchester and two postdoctoral fellows in the QuSys Group at Trinity, Mark Mitchison and Giacomo Guarnieri, the team studied very carefully an experimentally realistic erasure process that allows for quantum superposition (the qubit can be in state zero and one at same time).
Professor Goold explains: "In reality, computers function well away from Landauer's bound for heat dissipation because they are not perfect systems. However, it is still important to think about the bound because as the miniaturization of computing components continues, that bound becomes ever closer, and it is becoming more relevant for quantum computing machines. What is amazing is that with technology these days you can really study erasure approaching that limit.
"We asked, 'What difference does this distinctly quantum feature make for the erasure protocol?' And the answer was something we did not expect. We found that even in an ideal erasure protocol—due to quantum superposition—you get very rare events which dissipate heat far greater than the Landauer limit.
"In the paper, we prove mathematically that these events exist and are a uniquely quantum feature. This is a highly unusual finding that could be really important for heat management on future quantum chips—although there is much more work to be done, in particular in analyzing faster operations and the thermodynamics of other gate implementations.
"Even in 2020, Maxwell's demon continues to pose fundamental questions about the laws of nature."
More information: Harry J. D. Miller et al. Quantum Fluctuations Hinder Finite-Time Information Erasure near the Landauer Limit, Physical Review Letters (2020). DOI: 10.1103/PhysRevLett.125.160602
Journal information: Physical Review Letters
Provided by Trinity College Dublin