October 6, 2020 feature
A protocol to minimize the thermodynamic cost of erasing a single bit over a given amount of time
Stochastic thermodynamics theory is a framework that delineates the amount of heat, dynamics and entropy in small (i.e., mesoscopic) systems that are far from a state of thermodynamic equilibrium. In recent years, scientists have tried to use this theory to better understand the dynamics underlying a variety of systems, including colloidal particles, DNA, RNA, enzymes, molecular motors and electronic devices.
In a paper recently published in Physical Review Letters, researchers at Simon Fraser University combined stochastic thermodynamics with another construct known as optimal transport theory, with the aim of unveiling the thermodynamic cost associated with the erasure of a single bit of information from a device over a definite amount of time. Optimal transport theory is a framework introduced toward the end of the 18th century that answers questions such as: "If one has to move dirt from pile A to pile B, how should it be carried to minimize the effort required to transport it from one location to another?"
About a decade ago, theoretical physicist Erik Aurell and other researchers realized that optimal transport theory could also be used to solve a variety of optimization problems rooted in the field of thermodynamics. In their recent study, the team of researchers at Simon Fraser University performed calculations based on a technique introduced by Aurell and his colleagues.
"Our paper is based on the general framework of stochastic thermodynamics," Karel Proesmans, one of the researchers who carried out the study, told Phys.org. "By combining this theory with ideas from optimal transport theory, it is possible to calculate the minimum thermodynamic cost of a non-equilibrium process. We used these ideas to generalize Landauer's principle to finite-time processes."
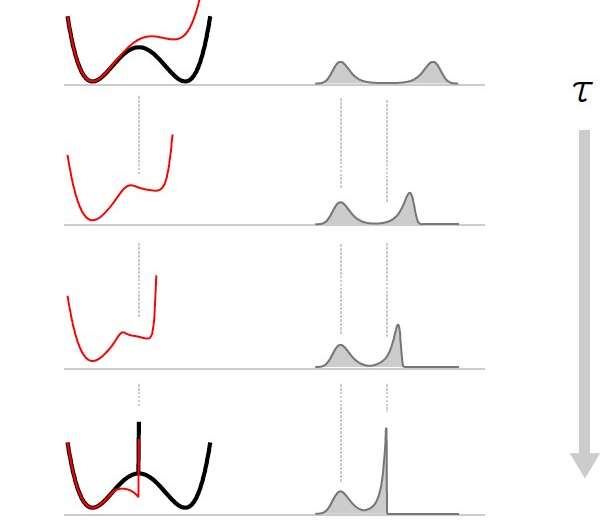
Landauer's principle, the primary principle outlining the thermodynamics of information processing, sets a lower theoretical limit for the energy consumed by a device when performing a given computation. It thus also provides a specific value that represents the minimum thermodynamic cost of erasing information from a device (i.e., kT ln2 per bit, where k is the Boltzmann constant and T is the temperature of the surrounding environment).
This minimum cost, however, is typically only achieved for operations that are performed very slowly. In their study, on the other hand, Proesmans and his colleagues set out to identify the most efficient way possible of erasing a bit from a device quickly within a set amount of time.
"We have derived protocols that minimize the work needed to erase a bit of information in a given amount of time, assuming we have complete control over the applied forces affecting the particle," Proesmans said. "In so doing, we also derived a simple lower bound on the amount of work needed to erase a bit."
The recent study carried out by Proesmans and his colleagues led to two important findings. First, the researchers were able to calculate lower and upper bounds on the minimum amount of work needed to erase a bit from a device. In the future, these bounds could serve as a reference for evaluating the performance of state-of-art devices and experimental platforms. Moreover, the framework proposed by the researchers could be used to construct optimal protocols for erasing bits from electronic devices.
"So far, we have focused on theoretical calculations," Proesmans said. "Our next step will be to test our bound on experimental systems. In particular, we will look at setups consisting of colloidal particles in optical tweezers. Another interesting question that we would like to answer is how well our bound changes when one has limited control over the system."
More information: Karel Proesmans et al. Finite-Time Landauer Principle, Physical Review Letters (2020). DOI: 10.1103/PhysRevLett.125.100602
Journal information: Physical Review Letters
© 2020 Science X Network