Octupole corner state in a three-dimensional topological circuit

Higher-order topological insulators featuring quantized bulk polarizations and zero-dimensional corner states are attracting increasing interest due to their strong mode confinement. Recently, scientists from China and the UK demonstrated in a 3-D topological circuit the existence of an octupole corner state, which is induced by the octupole moment of the bulk circuit and topologically protected by three anticommuting reflection symmetries. This work is not only of fundamental importance but also opens the door towards realizations of novel electronic topological devices.

Topological phases of matter have been one of the research interests in the field of condensed matter physics due to its unique properties in designing fascinating materials possessing quantized invariants in both electronics and photonics systems. These phases have shown great potential in lasing, quantum computing platform, and robust signal transmission in optics, acoustic, and mechanical systems. While most of the research interests of topological insulators have focused on observation of protected nontrivial mode localized at the surface of a bulk material, recent emergence of higher-order topological insulators (HOTIs) has led to discoveries of topological boundary states with dimensions lower than that of the bulk by more than 1. These quantized higher order multipole corner states are localized at the intersection of edges of a square (2-D, quadrupole moment) or cubic (3-D, octupole moment) lattice, and are protected by specially designed spatial symmetries. So far, the study of HOTIs are mostly limited to 2-D cases, and their corner states are either induced by the quadrupole moment or the 2-D Zak phase of the bulk lattice.

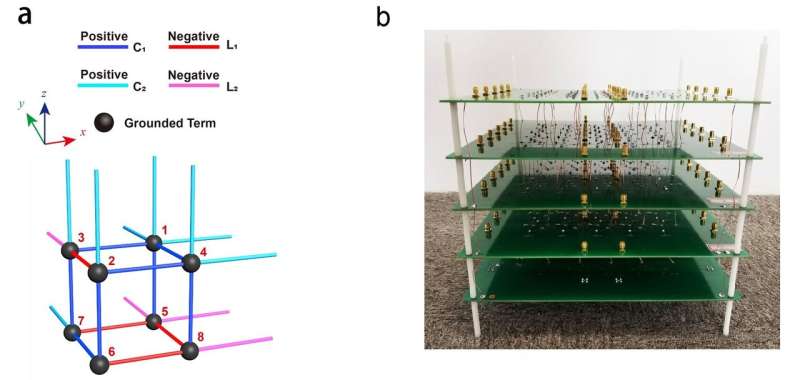
In a new paper published in Light Science & Applications, a team of scientists, led by Professor Shuang Zhang from School of Physics and Astronomy, University of Birmingham, United Kingdom, Prof Tiejun Cui from State Key Laboratory of Millimeter Waves, Southeast University, Nanjing, China, Prof. Yuanjiang Xiang from School of Physics and Electronics, Hunan University, Changsha, China and co-workers have reported the experimental observation of a 0-D corner state in a three-dimensional (3-D) topological circuit, which is built from a 3-D cubic network of inductors and capacitors with deliberately designed values. They verify that such corner state is induced by the nontrivial octupole moment of the 3-D circuit, and is topologically protected by three anticommuting reflection symmetries of the bulk lattice. This is achieved by engineering the dimerized coupling in each smallest loop (plaquette) in the circuit to have opposite sign to the other three, making this circuit a cubic lattice version of the famous Hofstadter model with π-flux per plaquette. "This is critical for generating a synthetic magnetic π-flux threading the plaquette that finally gives the octuple corner state in the finite-sized system," they emphasized.

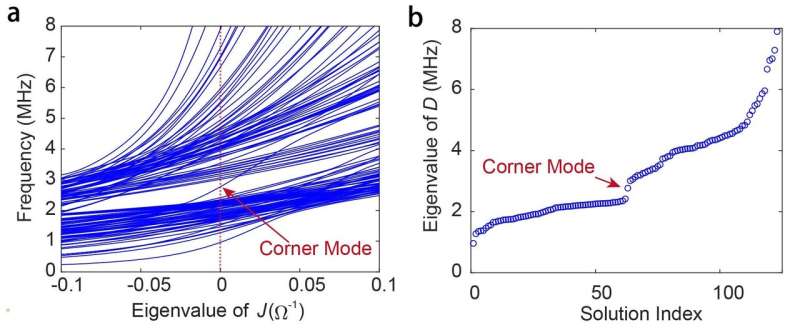
The topological features of the circuit were analyzed from the band structures of the circuit with both infinite and finite boundary conditions. This was achieved by constructing the circuit Laplacian and circuit Hamiltonian of the circuit based on the Kirchhoff law. They found an isolated midgap mode in the band gap of the finite band structure, which is the octupole corner state that is localized at the corner of the cubic circuit. To verify their theoretical prediction, they fabricated a sample that comprises of 2.5×2.5×2.5 unit cells (5×5×5 nodes) using five layers of circuit board, and measured the impedance spectra between every adjacent circuit node using a vector network analyzer (VNA). A distinct peak was clearly identified from the impedance spectrum at one of the circuit corners at exactly the corner mode frequency (2.77MHz), which was confirmed to be the octupole corner state they expected. The experimental results were in good agreement with the theoretical calculations for the impedance spectra at all the circuit nodes. To theoretically confirm the topology of the corner state observed in the simulation and experiment, they calculated the topological invariant of the circuit through a series of procedures called the nested Wilson loops, and obtained a quantized value of 1/2 and 0, which correspond to the nontrivial and trivial states, respectively.

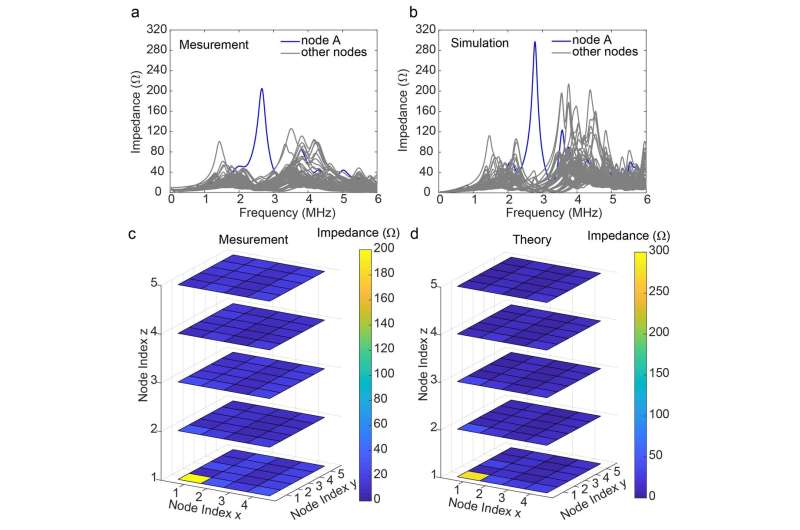
"Similar to the 1D edge state (2-D surface state) in conventional 2-D (3-D) topological materials, which exhibits excellent immunity against defects and disorder, the 0D corner state in our HOTI circuit is also highly robust against certain types of disorder." To evaluate the robustness of the octupole corner state, they provided the statistical distribution of the frequency of the corner state and the bandgap of the bulk from a number of disordered systems with different levels of variations in the circuit components. It was observed that the level of frequency shift of the corner mode is proportional to the randomness of the component variation, but its peak persists even at 20% circuit component variation. Further analyses were also performed to reveal the relationship between the bandgap and robustness of the corner state under different level of component disorder.

"The successful realization of octupole topological insulators paves the way for future investigations of higher-dimensional topological insulators possessing multipole moments without introducing synthetic dimensions, benefitting from the convenient electrical connections among nodes at arbitrary distances." The authors also mentioned that this work may provide an experimental platform for further investigation of 3-D higher-order topological circuit combined with non-Hermitian and nonlinear effects with the employment of active and nonlinear circuit devices such as operational amplifiers and varactor diodes.