July 1, 2020 feature
Programming van der Waals interactions with complex symmetries into microparticles using liquid crystallinity
Versatile approaches to engineer asymmetric van der Waals interactions can expand the palette of materials development through bottom-up engineering processes. In a new study, H.A. Fuster and a research team in chemical and biological engineering, and mathematics at the University of Wisconsin-Madison, Wisconsin, and Cornell University New York, U.S., demonstrated the polymerization of liquid crystals (LC) to program van der Waals interactions. They performed the experiments using a kinetically controlled probe colloid adsorption process and conducted complementary calculations to indicate that LC ordering could program van der Waals interactions across the surfaces of microparticles. They engineered the diverse LC configurations by confinement to provide fresh ideas in order to program van der Waals interactions, to assemble soft matter. The results are now published on Science Advances.
The assembly of particles into clusters and networks underlies the formation of different forms of soft matter including foams, emulsions, and thin-film coatings. While most studies in the past had focused on materials formed through interparticle interactions, recent studies have moved on to design soft materials via a bottom-up assembly of particles that encode anisotropic interparticle interactions. Van der Waals interactions are ubiquitous across all particulate systems and represent another promising approach to program the assembly of soft matter. In this report, Fuster et al explored an approach to control the symmetry of van der Waals interactions in particulate systems based on the synthesis of polymeric microparticles from liquid crystals (LCs). They described how the compositionally homogenous and spherical polymeric microparticles have well-defined patterns of orientational order to encode van der Waals interactions with complex symmetries.
Manipulating liquid crystals (LCs) confined in micro-scale domains.

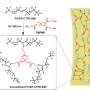
The team polymerized LC (liquid crystal) microdroplets prepared as oil-in-water emulsions to demonstrate how the internal orientational order could tune the spatial variation of van der Waals interactions across the surfaces of microparticles. They probed these interactions with a micron-sized polystyrene (PS) colloid. Van der Waals interactions collectively include dipole-dipole (Keesom), dipole-induced dipole (Keesom), dipole-induced dipole (Debye) and instantaneous dipole-induced dipole (London) interactions. The interactions can be calculated using the Lifshitz theory through low-frequency and high-frequency components of the dielectric response function relative to the constituting materials. Fuster et al used LCs to synthesize microparticles with desired internal orientational order and used that internal configuration to program complex yet predictable spatial patterns of van der Waals interactions. The results and calculations showed how LCs provided the basis to a versatile approach to program van der Waals interactions, similar to the conventional bottom-up assembly processes in materials science.
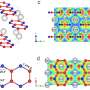
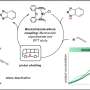
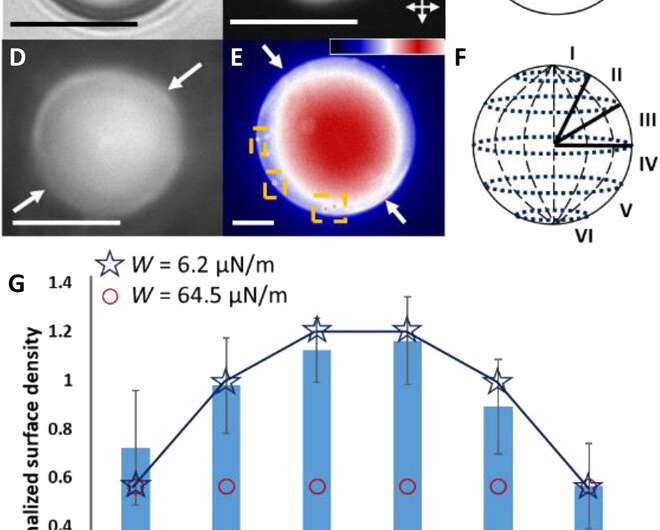
Previous studies had reported a remarkably diverse array of organization of LCs in microdroplets, which include chiral and achiral LCs formed from organic and aqueous phases. The team first examined achiral LCs formed via several different chemical mixtures in this work, where the compounds had anisotropic dielectric response functions. The team then dispersed the LC mixture into glycerol and formed micron-sized LC droplets with a bipolar configuration. The polymeric microparticles preserved the bipolar configuration of LC droplets from which they were formed after photopolymerization as confirmed with bright-field and polarized light micrographs. The scientists then mapped the spatial variation of the van der Waals interactions across surfaces of polymerized bipolar microparticles by reversibly adsorbing polystyrene probe colloids (1 µm diameter) on such microparticle surfaces.
Investigating van der Waals interactions between the probe colloids and microparticles.

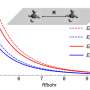
They interpreted the experimental observations relative to van der Waals interactions between the probe colloids and LC microparticles. For instance, the team quantified the distribution of probe colloids adsorbed on surfaces of bipolar microparticles in the presence of salt water, where the number increased with time in a kinetically controlled aggregation process. For control experiments, they repeated the methods using LC (liquid crystal) microparticles polymerized in the radial configuration. Based on the results, Fuster et al hypothesized that the patterning of probe colloids on bipolar microparticles arose from the van der Waals interactions encoded through orientational ordering of molecules within the bipolar microparticles. They supported the hypothesis with calculations to indicate that the orientations of LCs within microparticles could be used to encode sufficiently large variations in van der Waals interactions, allowing for direct bottom-up assembly of soft-matter systems.
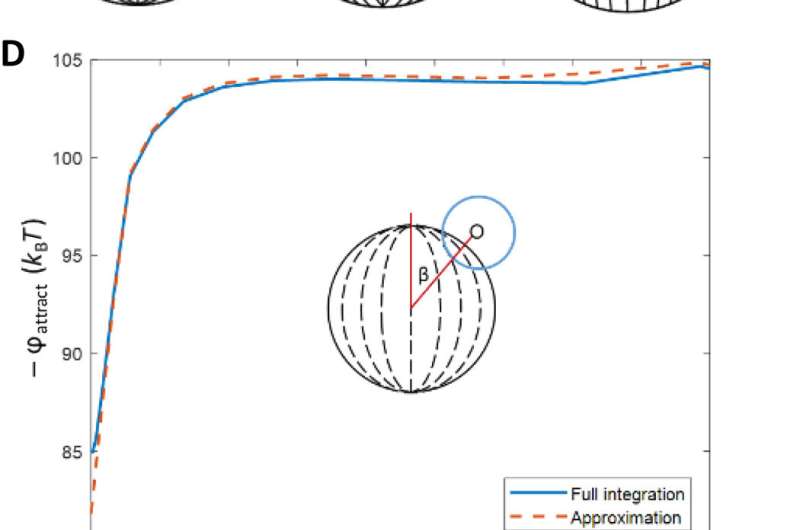
The team then investigated the theoretical predictions of bipolar LC microparticle internal ordering and calculated their attractive interaction energies. They noted the van der Waals interactions between the probe colloids and the bipolar microparticles to be stronger at the equatorial region, and consistent with experimental observations. The change in dielectric response experienced by a probe colloid near a bipolar microparticle acted as a strong anchoring energy and van der Waals interactions were particularly sensitive to such surface anchoring energies.
Fuster et al. then studied the net interaction energy between a probe colloid and the polymerized bipolar microparticles as the sum of attractive van der Waals and repulsive double-layer interactions. For additional support on their hypothesis that van der Waals interactions can be encoded by internal configurations of LC microparticles, the team prepared LC microparticles with dipolar symmetry. They noted the zeta potential measurements of these microparticles to yield values similar to the polymerized bipolar LC microparticles. Based on the experimental outcomes, Fuster et al. confirmed that manipulating the LC ordering within the microparticles provided a versatile approach to pattern van der Waals interactions across the surfaces of microparticles.
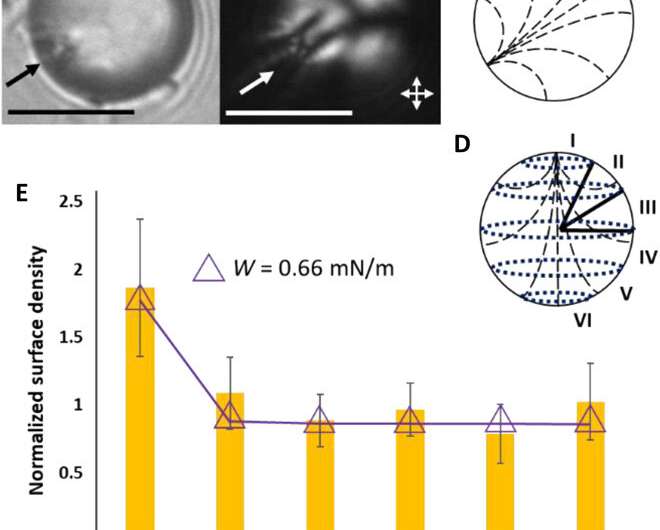
In this way, H.A. Fuster and colleagues characterized anisotropic van der Waals interactions programmed into microparticles by controlling the internal LC ordering and quantifying kinetically controlled colloid adsorption across the surface of the LC microparticles. The experiments and supporting calculations showed the spatial variation of van der Waals interactions across the surfaces of LC microparticles to be as large as 20 KBT. This magnitude is large enough to engineer the bottom-up assembly of soft materials. The scientists interpreted the experimental observations relative to van der Waals interactions between LC (liquid crystal) microparticles and probe colloids. The results established the basis for a general and simple approach to program van der Waals interactions into colloidal soft matter systems, since the scientists could vary the ordering of LCs and manipulate them in a range of experimental geometries. The principles of this study will be applicable to a range of soft matter phenomena including adhesion and wetting surfaces, including the formation of colloidal assemblies such as glasses, crystals, and gels.
More information: H. A. Fuster et al. Programming van der Waals interactions with complex symmetries into microparticles using liquid crystallinity, Science Advances (2020). DOI: 10.1126/sciadv.abb1327
Sharon C. Glotzer et al. Anisotropy of building blocks and their assembly into complex structures, Nature Materials (2007). DOI: 10.1038/nmat1949
C. A. Silvera Batista et al. Nonadditivity of nanoparticle interactions, Science (2015). DOI: 10.1126/science.1242477
Journal information: Science Advances , Nature Materials , Science
© 2020 Science X Network