May 7, 2020 feature
Finite-temperature violation of the anomalous transverse Wiedemann-Franz law
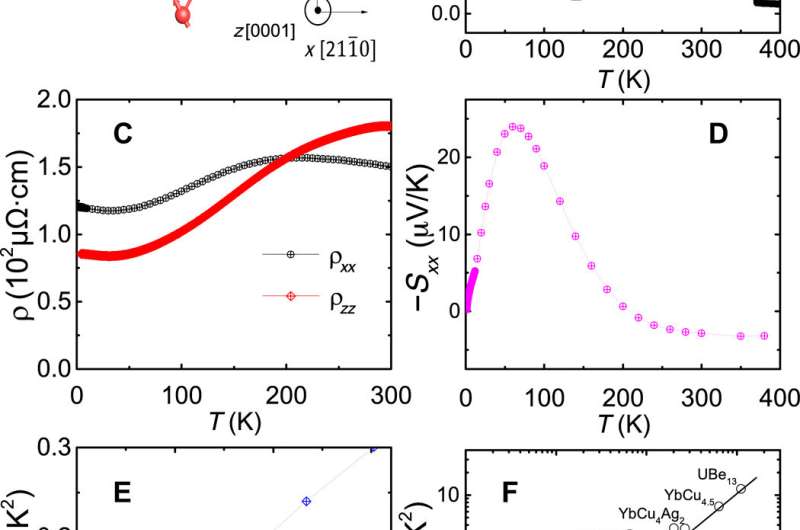
![Anomalous transverse coefficients, definitions, and profiles: Off-diagonal components of the three conductivity tensors [electric (σ̄ ), thermoelectric (ᾱ ), and thermal (κ̄ )] can be finite in the absence of magnetic field. As shown in the three left panels, they link to four vectors, which are charge density current (J→), electric field (E→), thermal gradient (∇→T), and heat density current (JQ−→). (A) Hall resistivity (ρzx). (B) Hall conductivity (σzx) extracted from ρzx, ρxx, and ρzz. (C) Nernst signal (Szx). (D) Transverse thermoelectric conductivity (αzx) extracted from Szx, Sxx, ρxx, ρzz, and ρzx. (E) Thermal Hall resistivity (Wzx). (F) Thermal Hall conductivity or the Righi-Leduc coefficient (κzx) extracted from off-diagonal and diagonal thermal resistivities. Credit: Science Advances, doi: 10.1126/sciadv.aaz3522 Finite-temperature violation of the anomalous transverse Wiedemann-Franz law](https://scx1.b-cdn.net/csz/news/800a/2020/finitetemper.jpg)
According to the Wiedemann-Franz (WF) law, the electrical conductivity of a metal is linked to its thermal counterpart, provided that the heat carried by the phonons is negligible and the electrons do not suffer inelastic scattering. In a type II Weyl semimetal also known as a fourth fermion, the thermal dependence of the ratio between electrical and thermal conductivity highlights deviations from the Wiedemann-Franz law. Physicists have tested the WF law in numerous solids but intend to understand the extent of its relevance during anomalous transverse transport and investigate the topological nature of the wave function. In a new report, Liangcai Xu and an international research team in condensed matter physics in China, France, Israel and Germany, presented a study of the anomalous transverse response in a noncollinear antiferromagnetic Weyl semimetal, Mn3Ge. They varied the experimental conditions from room temperature down to sub-Kelvin temperature and observed finite-temperature violation of the WF correlation. They credited the outcome to a mismatch between the thermal and electrical summations of the Berry curvature (a geometric phase acquired within the course of a cycle) and not due to inelastic scattering. The team backed their interpretation with theoretical calculations to reveal a competition between the temperature and Berry curvature distribution. The work is now published on Science Advances.
The Berry curvature of electrons can result in the anomalous Hall effect (AHE) if the host solid lacks time-reversal symmetry (conservation of entropy). While the thermoelectric and thermal counterparts of the anomalous Hall effect are explored less frequently, they too arise from the same fictitious magnetic fields. It remains to be determined how the magnitudes of such anomalous off-diagonal coefficients correlate with each other and if the established correlations between ordinary transport coefficients continue to hold. It is currently laborious to form a semiclassical formula of the anomalous Hall effect (AHE), thereby making any intuitive picture of producing a transverse electric field even more challenging. In this work, the research team presented a study of a magnetic solid, focused on the relation between anomalous electrical and thermal Hall conductivities. Xu et al. determined the variables across a wide temperature range, to include the anomalous Lorenz ratio (LAij) and the Sommerfeld value (L0), which remained close to each other, however a deviation started above 100 K. The team claimed that the observation implied a hitherto unobserved mechanism for finite-temperature violation of the WF law. As a result, they supported experimental observations in the study with theoretical calculations to identify the Berry curvature of the Weyl semimetal family (Mn3Ge and Mn3Sn).
Based on theoretical propositions, the team observed a large anomalous Hall effect in Mn3X (where X equalled Sn and Ge) family of noncollinear antiferromagnets below a Néel temperature i.e. reflecting the nonlinearity of superparamagnetic materials in low-fields. The results provided a distinct profile on Hall resistivity and a straightforward method to extract the anomalous conductivity with the newcomers (Mn3Ge and Mn3Sn) in the emerging field of antiferromagnetic spintronics. The scientists even followed the fate of the signals in Mn3Ge down to sub-Kelvin temperatures in the study to understand the phenomenon.
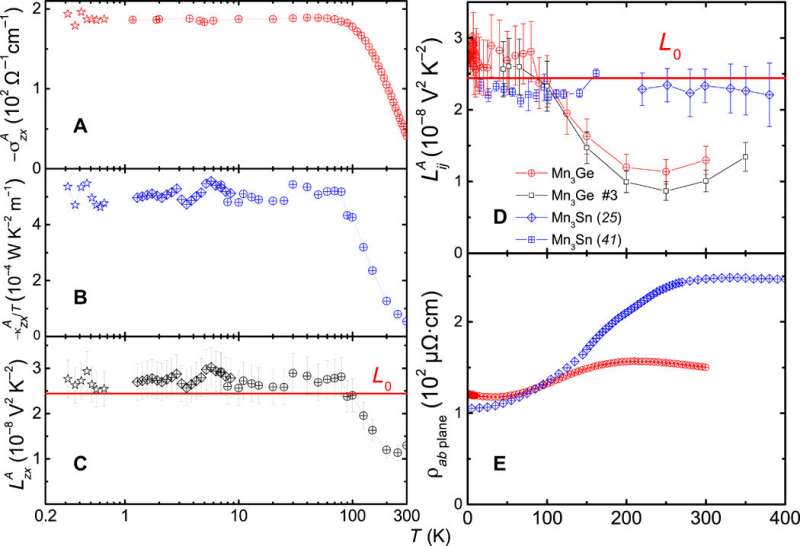
They measured the Hall resistivity, Nernst signal (thermoelectric or thermomagnetic phenomenon observed in a sample conducting electricity—subject to a magnetic field) and thermal Hall resistivity to extract electric/thermoelectric and thermal Hall conductivities. They observed basic properties of the system, including the spin texture, magnetization and the electrical resistivity to show little variation with temperature. Xu et al. detailed the anomalous transverse WF law as the main finding of the study. For instance, below 100 K, the anomalous Lorenz ratio was flat with a magnitude slightly larger than the Sommerfeld value. Above 100 K, the anomalous Lorenz ratio in Mn3Ge and Mn3Sn behaved very differently but their resistivity only showed a slight change with temperature, in contrast to elemental ferromagnets.
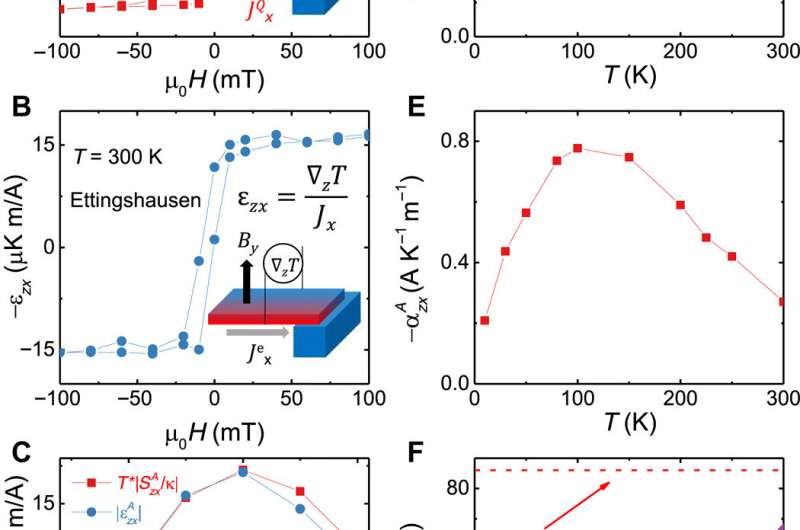
Since several previous propositions on the violation of WF law were later refuted, the new data had to be validated by independent criteria. The scientists supported the validity of their work by verifying the Kelvin relation (for normal transport coefficients) and the Bridgman relation (for anomalous transverse coefficients). Based on the thermodynamics of irreversible processes, the relations had to remain valid regardless of microscopic details. Xu et al. therefore incorporated the same data (electric field and thermal gradient) for thermal and thermoelectric studies and the resulting validity of Kelvin and Bridgman relations in the work guaranteed the validity of the collected thermal data as further experimental confirmation.
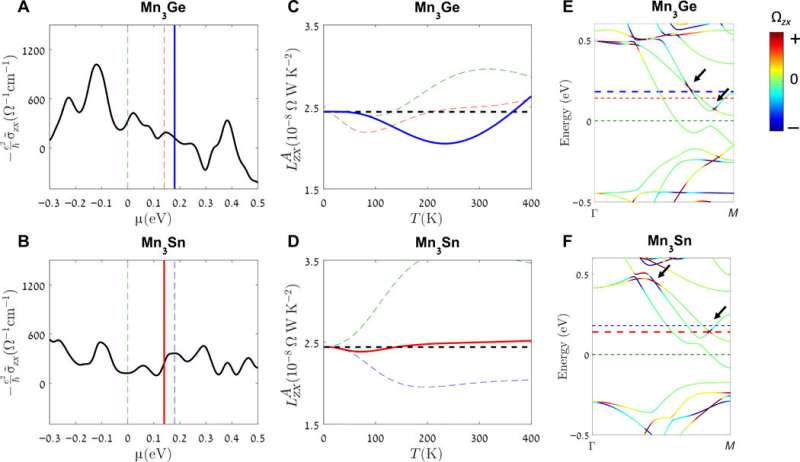
The WF law can also cease to be valid in the presence of inelastic scattering, since small-angle inelastic collision can decay the momentum flow. When the team examined the case of Mn3X metals relative to the WF law they concluded the dominant scattering mechanisms in both Mn3Sn and Mn3Ge to be based on scattering off antisite defects (crystallographic defects). There was little room for inelastic scattering in the study, highlighting the requirement for an alternative route toward the observed violation of the WF law. The resulting theory qualitatively showed the different Berry spectrum in Mn3Sn and Mn3Ge, which lead to different behaviors at finite temperature for the two compounds; thereby meeting the alternative route requirement and further validating the outcome of the study.
In this way, Liangcai Xu and colleagues measured counterparts of the anomalous Hall effect associated with the flow of entropy. They found WF law linking the thermal and electrical Hall effects to be valid at zero temperature, although a finite deviation emerged above 100 K. The dominant scattering effect in the study was elastic and they proposed the deviation to result from a mismatch in thermal and electrical summations of the Berry curvature alongside theoretical calculations, which additionally supported the work.
More information: Liangcai Xu et al. Finite-temperature violation of the anomalous transverse Wiedemann-Franz law, Science Advances (2020). DOI: 10.1126/sciadv.aaz3522
Libor Šmejkal et al. Topological antiferromagnetic spintronics, Nature Physics (2018). DOI: 10.1038/s41567-018-0064-5
K. Kuroda et al. Evidence for magnetic Weyl fermions in a correlated metal, Nature Materials (2017). DOI: 10.1038/nmat4987
Journal information: Science Advances , Nature Physics , Nature Materials
© 2020 Science X Network