October 31, 2019 feature
A theoretical explanation for an enhanced thermal Hall response in high-temperature superconductors
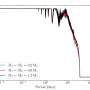
A few months ago, a team of researchers led by Louis Taillefer at the University of Sherbrooke measured the thermal Hall conductivity in several compounds of copper, oxygen and other elements that are also high-temperature superconductors known as 'cuprates.' In physics, the thermal Hall effect describes heat flow in a direction transverse to a temperature gradient.
Generally, heat flows in the same direction as the temperature gradient, but in the presence of a magnetic field, some flows in the transverse direction, too; this is known as the thermal Hall effect. In their study, Taillefer and his collaborators observed that in the cuprates, this transverse flow can sometimes be very large, which was surprising for many physicists worldwide.
Inspired by this observation, a team of researchers at Harvard University and the University of California recently set out to investigate it further. In their paper, published in Nature Physics, they were able to explain these striking findings by taking into account the possibility that the applied magnetic field in the experiment could bring the material close to an exotic phase with a large thermal Hall conductivity.
Essentially, the large signal observed by Taillefer and his colleagues indicates the presence of other mobile degrees of freedom that, unlike usual electrons, do not carry an electric charge, but contribute to the thermal Hall conductivity. These additional degrees of freedom only appear to be present in the Néel state and in the so-called 'pseudogap' state.
The Néel state is a state in which there is one electron per square lattice site and electron spins are arranged in opposite directions like black and white squares on a chess board. The pseudogap state, on the other hand, one of the most mysterious states in the phase diagram of high-temperature superconductors, emerges when the Néel order is destroyed by doping the system with holes (i.e., reducing the electronic density from one electron per square lattice site).
"These observations immediately caught our attention since our previous theoretical attempts to understand the phase diagram of the cuprates, which were motivated by a set of very different measurements and numerical simulations, naturally involve mobile 'spinon' excitations inside the pseudogap phase," Mathias Scheurer and Subir Sachdev, two of the researchers who carried out the study, told Phys.org. "Spinons carry spin but no charge, and hence represent a natural source of the observed large thermal Hall response. We were thus eager to analyze whether these theoretical descriptions can quantitatively reproduce the thermal Hall data of Taillefer's group."
To investigate whether the theoretical constructs they devised were aligned with the data gathered by Taillefer and his colleagues, the researchers first focused their theoretical investigations on the undoped cuprates, with one electron per site and Néel order. They chose to study this particular system because undoped experimental samples are the cleanest, and thus, the experimental signatures in Taillefer's data are most likely intrinsic for the undoped samples, rather than a consequence of inhomogeneities in the system. In addition, the observations gathered by Taillefer and his team for the undoped system are also most surprising, as they undermined the previous understanding of the Néel phase.
"Both we and P. Lee's group concluded after detailed investigations that conventional spin-wave theory cannot reproduce the large thermal Hall response seen in experiment," Scheurer and Sachdev said. "Therefore, one is faced with the problem of finding a mechanism for the observed enhanced thermal Hall effect in the Néel phase, which we address in our recent Nature Physics article."
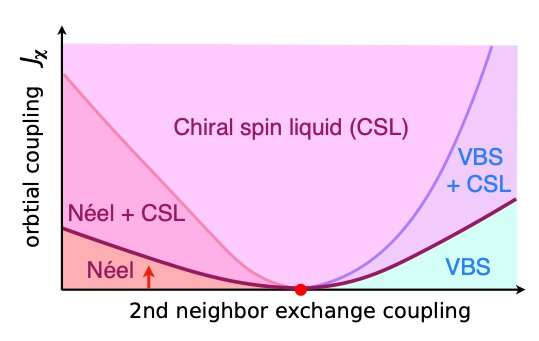
One key aspect of the explanation for the thermal Hall effect provided by Scheurer, Sachdev and their colleagues is the orbital coupling Jχ of the magnetic field. In materials with very strong interactions, such as cuprates, this orbital coupling is often neglected, as it is expected to be significantly weaker than the direct coupling of the spin to the magnetic field, which is known as Zeeman coupling. However, in the proximity of a critical point, its effect can be enhanced significantly.
"Our theory is that a small Jχ can drive the system into a chiral spin liquid (CSL) phase in the vicinity of the critical point—an effect we expected to be further enhanced in the presence of spin-orbit coupling," Scheurer and Sachdev said. "CSLs are related to quantum Hall phases, with the crucial difference that the mobile degrees of freedom are not electrons but rather spinons, which only carry spin and no electric charge. As such, they do not exhibit a quantized electric Hall response, but by virtue of carrying energy, yield a quantized thermal Hall response."
The theory devised by Scheurer, Sachdev and their colleagues suggests that the magnetic field applied in experiments investigating the thermal Hall effect drives the Néel phase in proximity to a CSL that coexists with Néel order. In their study, they found that although the undoped system remained in the Néel phase, this proximity yields a large thermal Hall response similar, but somewhat smaller, than that observed in the data of Taillefer's team. The researchers also observed that the dependence they predicted for the thermal Hall conductivity on both temperature and magnetic field agrees well with the measurements.
The theory proposed by the researchers thus represents a natural possible explanation of the striking observations of Taillefer and his colleagues. This thermal Hall conductivity cannot be explained by the spin-wave theory of the Néel state, which was previously believed to capture the physics of the undoped compounds very well.
"Our work indicates that spinon excitations have to be taken into account, even in the Néel phase," Scheurer and Sachdev said. "Our study also illustrates that the orbital coupling of the magnetic field, although expected to be weak compared to the Zeeman coupling, can play a key role."
In addition to providing a feasible explanation for the findings gathered by Taillefer and his colleagues, Scheurer, Sachdev and their colleagues came up with an effective theory for the transition between the Néel state and the CSL. This theory has four different 'dual' formulations. In other words, there are four theories that look very different at first sight (e.g., they contain different types of elementary degrees of freedom), but essentially describe the same physics.
"In our work, we could relate all four theories to the microscopic degrees of freedom of the undoped cuprates," Scheurer and Sachdev explained. "It is quite exciting to see how abstract statements of 'dualities' between theories obtain a concrete representation in a real material with direct consequences for condensed matter experiments. We hope that the insights of our recent work will prove useful for the extension to the doped system."
So far, the team of researchers at Harvard University and the University of California was able to provide a viable theoretical explanation of why the undoped cuprate compounds present an enhanced thermal Hall response. In their future work, they plan to investigate this topic further by elaborating on the four different 'dual theories' they proposed for the enhancement mechanism of the thermal Hall effect.
"As our previous computations are only based one description, we are planning to look into the respective predictions for the thermal Hall conductivity in the three other theories; this is also expected to advance our understanding of the physics behind the underlying dualities," Scheurer and Sachdev said. "Another important problem for future research will be extending our analysis to the doped system. This will likely shed light on the nature of the pseudogap phase."
More information: Rhine Samajdar et al. Enhanced thermal Hall effect in the square-lattice Néel state, Nature Physics (2019). DOI: 10.1038/s41567-019-0669-3
G. Grissonnanche et al. Giant thermal Hall conductivity in the pseudogap phase of cuprate superconductors, Nature (2019). DOI: 10.1038/s41586-019-1375-0
Mathias S. Scheurer et al. Topological order in the pseudogap metal, Proceedings of the National Academy of Sciences (2018). DOI: 10.1073/pnas.1720580115
Rhine Samajdar et al. Thermal Hall effect in square-lattice spin liquids: A Schwinger boson mean-field study, Physical Review B (2019). DOI: 10.1103/PhysRevB.99.165126
Jung Hoon Han et al. Consideration of thermal Hall effect in undoped cuprates, Physical Review B (2019). DOI: 10.1103/PhysRevB.99.205157
Journal information: Nature Physics , Nature , Proceedings of the National Academy of Sciences , Physical Review B
© 2019 Science X Network