Physicist estimates the effect of dark matter on the shadow of a black hole
A RUDN University physicist has developed a formula for evaluation of the effect of dark matter on the size of the shadow of a black hole. It turned out that the effect would be noticeable only if the concentration of this hypothetical form of matter around black holes in the centers of galaxies is abnormally high. If it is not the case, then it is unlikely that dark matter could be detected using the shadow of a black hole. The work was published in the journal Physics Letters B: Nuclear, Elementary Particle and High Energy Physics.
In April 2019, the Event Horizon Telescope received the first-ever image of the shadow of a supermassive black hole located in the center of the M87 galaxy. To get this shot, astronomers had to combine eight observatories located around the globe. The image does not have sufficient resolution to clearly define the geometry of the central black hole, but researchers hope to achieve higher quality in the future. Determining the shape of its shadow will allow astronomers to test various versions of the theory of gravity and, possibly, find a "bridge" that would combine quantum mechanics and the general theory of relativity.
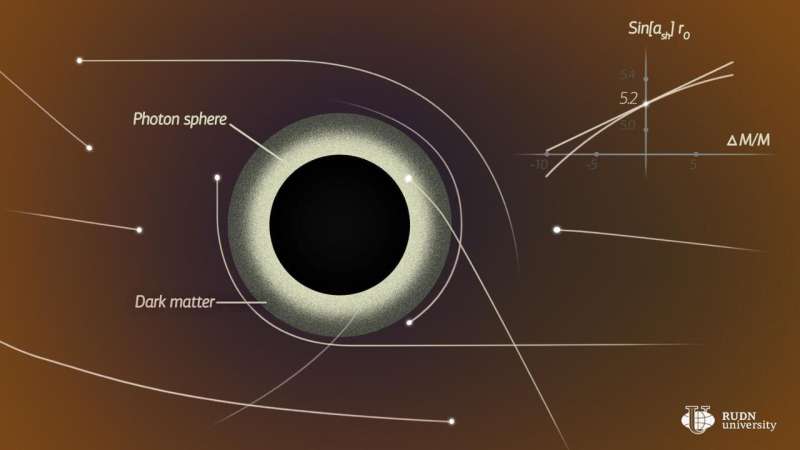
Roman Konoplya, an associate professor of the Educational and Scientific Institute of Gravity and Cosmology of the RUDN University, wondered if hypothetical dark matter, which accounts for about 85 percent of all matter in the universe, can have a visible effect on the shape and radius of the shadow of a black hole—a dark spot that appears due to the curvature of the trajectories of photons in the super-powerful gravitational field of such an object. The cosmologist obtained a formula that makes it possible to determine the change in the radius of the shadow depending on the amount of dark matter surrounding it.
The RUDN cosmologist examined a simple spherical model of a non-rotating (Schwarzschild) black hole surrounded by a halo of dark matter. Then he developed a general formula for measuring the radius of the shadow of a black hole by considering the equation of the space metric for the case of dark matter.
The solutions of the equation depend on the relative position of the photon sphere and the scattered shell of dark matter—the halo. The photon sphere is the smallest radius of the photon's orbit around a black hole. A photon in this orbit can no longer leave the vicinity of the hole but does not yet fall into it.
There can be three options for such a mutual spatial arrangement. The first is that dark matter is distributed in such a way that the photon sphere lies between the layer of dark matter and the event horizon. In this case, the size of the shadow of the black hole would not change for the observer, and we will not be able to detect the presence of dark matter by the shape of the shadow. The second one—when the halo of dark matter is closer to the event horizon than the photon sphere—is impossible, since all matter in this area will inevitably be absorbed by the black hole.
The third option is the most interesting: The photon sphere is immersed in a halo of dark matter. In this case, the radius of the shadow would depend on the density of the layer of dark matter and on its mass: The smaller the density and the higher the mass, the greater the radius of the shadow. However, the calculations performed by the RUDN cosmologist showed that for the change in the radius of the shadow of the black hole to be noticeable to an outside observer, an abnormally high concentration of dark matter around the central black hole is required. Roman Konoplya concluded that the influence of dark matter on the radius of the shadow is likely to be imperceptible.
"In order to deform the geometry of the black hole so much that it will be noticeable from observations of the shadow, dark matter should be concentrated near the black hole. In our galaxy, there are, according to some estimates, about 100 billion solar masses of dark matter. However, it is assumed that dark matter is distributed throughout the galactic halo and not only in its center. To influence the shadow of a black hole, all this huge mass must be concentrated in the central region, which occupies approximately one-millionth of its total volume," Roman Konoplya explained.
The negative result, which means that modern astronomers would not be able to use black holes as a "detector" of dark matter, is extremely important for astrophysicists who are engaged in its search. Dark matter is a hypothetical form of matter, which makes up about 85 percent of the matter of the universe and about 25 percent of its density, by modern estimates. Dark matter does not emit electromagnetic radiation, unlike ordinary baryonic matter, and does not directly interact with it. Therefore, despite all efforts, astronomers still have not been able to obtain direct evidence of its existence.
But if an abnormally high concentration of dark matter around a black hole turns out to be possible for some reason, astronomers will need to consider models that also take into account the effects of the rotation of the black hole and the dark matter surrounding it.
More information: R.A. Konoplya. Shadow of a black hole surrounded by dark matter, Physics Letters B (2019). DOI: 10.1016/j.physletb.2019.05.043
Journal information: Physics Letters B
Provided by RUDN University