August 12, 2019 feature
Patterns typically observed in water can also be found in light

Sometimes in shallow water, a type of wave can form that is much more stable than ordinary waves. Called solitons, these phenomena emerge as solitary waves and can travel long distances while maintaining their shape and speed, even after colliding with other waves.
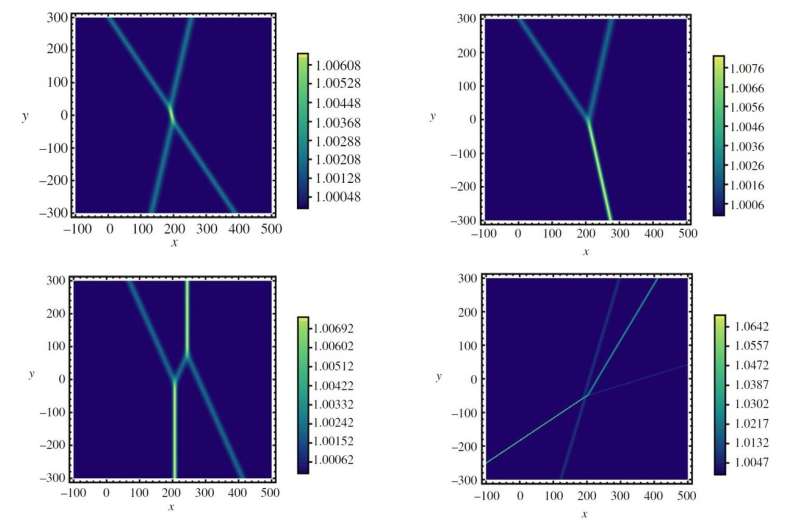
However, in certain cases soliton collisions can generate complicated wave patterns, sometimes called "alphabet waves" since they resemble the letters X, Y, and H, as well as combinations of these shapes. Soliton waves and their collision patterns have fascinated scientists ever since they were discovered in the 19th century.
Now in a new study, researchers have discovered that that these same patterns in water waves also emerge in collisions of optical solitons (light waves with the same stable properties). The researchers show that the same equation, called the Kadomtsev-Petviashvili II (KPII) equation, that is used to model water soliton interactions can also be used to model optical soliton interactions, revealing a close connection between the wave dynamics of water and light.
Theodoros P. Horikis, at the Department of Mathematics, University of Ioannina, and Dimitrios J. Frantzeskakis, at the Department of Physics, University of Athens, have published a paper on the patterns in optical solitons in a recent issue of Proceedings of the Royal Society A.
"We all have been on a beach and noticed the intricate patterns that waves form in the shallow, near the shoreline: beautiful X-, Y-, and even H-shaped waveforms frequently emerge out of the interaction of straight waves," Horikis told Phys.org. "Remarkably, these phenomena are fully understood and can be described mathematically in detail using appropriate mathematical models. Surface tension, which is the phenomenon that causes fluids to minimize the area they occupy, plays a major role in the formation of X-, Y-, and H-shaped waves. In water, surface tension is small, while in mercury, for example, surface tension is large.
"We have shown that optical soliton propagation in nonlocal media—which include plasmas, nematic liquid crystals and liquid solutions with thermal nonlinearities—is governed by the same model that is used to describe shallow waters, with nonlocality playing the role of surface tension. Thus, indeed, 'light meets water,' as we predict that X-, Y-, H-shaped, and even more complicated wave structures that we observe in flat beaches can also be observed in optics, as optical beams propagating in nonlocal nonlinear media."
As the researchers explained, an optical medium is nonlocal when its response to light depends not only on the position where the external optical field is applied (as in a local medium), but also on the total surface and volume of the medium. In nonlocal media, light that strikes at a certain point is carried away to the surrounding region, so that a narrow localized optical beam can induce a spatially broad response of the medium. The analogy between the weak surface tension of water and strong nonlocality in certain optical media is what enables the description of optical solitons in terms of the KPII equation.
"What is important in our article is that these two phenomena, nonlocality in optics and surface tension in water, seem to have a one-to-one correspondence, so to speak," Horikis said. "Importantly, optical solitons that would be unstable in media with weak nonlocality, or in fluids with strong surface tension (such as mercury), can become stable in strongly nonlocal optical media. Due to this important stabilization effect induced by the strong nonlocality, the host optical medium can support solitons much like the surface of water, whose contact with air acts as a thin elastic sheet on which these 'alphabet waves' can form!"
Based on this result, the researchers used numerical simulations to model collisions of two or three optical solitons. Similar to the water soliton case, they found that X-, Y-, and H-shaped waves emerged, and also that the angle of interacting solitons leads to different patterns.
The researchers expect that it may be possible to experimentally observe these optical soliton patterns by using technology recently used to observe individual solitons. This would require combining two solitons inside a nonlocal medium—for example, a nematic liquid crystal—while using mirrors to control the angle between the two light beams used to generate the solitons.
Their findings suggest that in the future it may also be possible to find even more intricate patterns, such as web-like structures of waves, in collisions of optical solitons. They also plan to investigate whether other highly nonlocal systems, such as Bose-Einstein condensates (macroscopic quantum systems composed by ultracold atoms) and colloids (mixtures containing particles suspended in solution), may also provide the necessary ingredients to support the emergence of these patterns.
More information: Theodoros P. Horikis and Dimitrios J. Frantzeskakis. "Patterns of water in light." Proceedings of the Royal Society A. DOI: 10.1098/rspa.2019.0110
Journal information: Proceedings of the Royal Society A
© 2019 Science X Network