August 1, 2019 feature
Measurements induce a phase transition in entangled systems
Many famous experiments have shown that the simple act of observing a quantum system can change the properties of the system. This phenomenon, called the "observer effect," appears, for example, when Schrödinger's cat becomes either dead or alive (but no longer both) after someone peeks into its box. The observation destroys the superposition of the cat's state, or in other words, collapses the wave function that describes the probabilities of the cat being in each of the two states.
In a new paper, physicists have further investigated exactly how measurements affect quantum entanglement, which in this context is equivalent to the extent to which a system is in a superposition. Previous studies have shown that, when a quantum system is left alone to evolve without any outside interference, its degree of entanglement tends to increase. That is, quantum systems tend to drift over time into states with a large degree of quantum superposition.
On the other hand, making a measurement on an entangled state tends to decrease its entanglement. This happens because a measurement on a spin state (for example) collapses that spin into a definite state, which causes that spin to become disentangled from the other spins, whose states remain in a superposition. This reduces the amount of entanglement in the system overall.
In the new paper, the physicists have demonstrated via computer simulations and theoretical arguments that, when measurements are made at a rate that exceeds a critical value, a measurement-induced phase transition occurs. This causes the system to sharply transition from an "entangling" phase, in which the amount of entanglement grows continuously over time, to a "disentangling" phase, in which some entanglement still exists, but its growth rate drops to zero.
The physicists, Brian Skinner at MIT, Jonathan Ruhman at MIT and Bar-Ilan University, and Adam Nahum at Oxford University, have published their paper on the phase transition for entanglement in a recent issue of Physical Review X.
"One of the great successes of physics is its ability to describe phase transitions—the abrupt change of material properties when some external parameter is varied, like water suddenly freezing into ice when it drops below 32 degrees Fahrenheit," Skinner told Phys.org. "What we have shown is that this same language can be applied to a dynamical process involving quantum entanglement. That is, the dynamical properties of entanglement growth also have a phase transition as a function of an external parameter, which is the rate at which measurements occur. For us, this is a beautiful and surprising connection!"
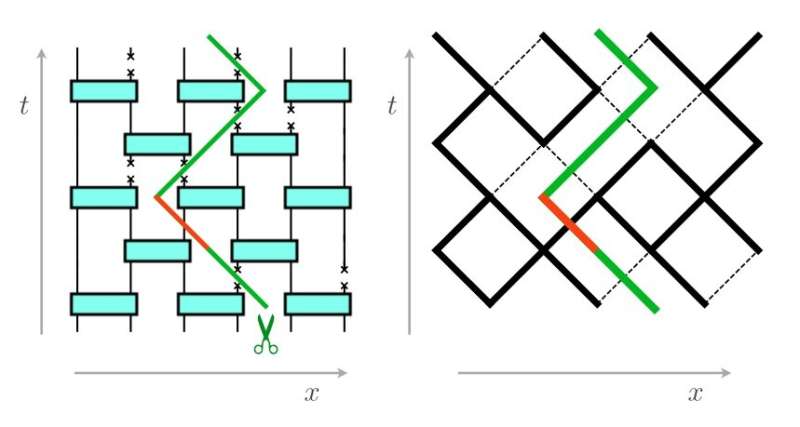
The researchers developed a model of this measurement-induced phase transition based on a famous problem from percolation theory called the "vandalized resistor grid." In this problem, a vandal tries to find the smallest number of bonds (call the "shortest path" or "minimal cut") to slice through an electric grid in order to completely disconnect the network. The researchers showed that the problem of calculating the entropy of entanglement in a quantum system is equivalent to this optimization problem, in which the goal is to find a minimal cut through a disordered network that separates the network into two parts.
In an entangled system, the network represents the quantum system, and each measurement represents breaking one of the bonds. The degree of entanglement in the system is determined by the size of the minimal cut in this network, i.e., the total number of unbroken bonds that must be broken in order to separate the system from the rest of the network. In a sense, this number tells how frequently measurements can be made before an entangled system transitions into the disentangled phase. As different networks have different numbers and arrangements of bonds, the critical measurement rate differs for different systems.
The physicists expect that an understanding of this measurement-induced phase transition in entanglement dynamics may have useful implications for developing simulations of quantum systems. Entanglement plays an important role in determining the difficulty of simulating quantum dynamics on a classical computer. As a result, the entangled-to-disentangled phase transition implies the existence of an easy-to-hard transition for simulations. This may allow researchers to better predict the difficulty of simulations and look for easier alternatives.
"Our finding has an immediate implication for the question of how hard it is to simulate quantum systems using classical computers," Skinner said. "It may also be important for quantum computing schemes, which often rely on maintaining long-range entanglement."
In the future, the researchers plan to investigate how universal their model is.
"There are different ways of describing quantum entanglement mathematically," Skinner said. "What we showed was that one of these descriptions is perfectly analogous to a classical percolation problem. But right now it's unclear how generic this analogy is, and whether other ways of describing entanglement belong to the same 'universality class.' The first priority right now is to establish whether the analogy is only an approximate one that works in some contrived situations, or whether it is completely generic across a wide range of descriptions and experimental setups."
See Dr. Skinner's Twitter posts on the paper.
More information: Brian Skinner, Jonathan Ruhman, and Adam Nahum. "Measurement-Induced Phase Transitions in the Dynamics of Entanglement." Physical Review X. DOI: 10.1103/PhysRevX.9.031009
Journal information: Physical Review X
© 2019 Science X Network