A quantum leap in particle simulation
A group of scientists at the Department of Energy's Fermilab has figured out how to use quantum computing to simulate the fundamental interactions that hold together our universe.
In a paper published in Physical Review Letters, Fermilab researchers fill a conspicuous gap in modeling the subatomic world using quantum computers, addressing a family of particles that, until recently, has been relatively neglected in quantum simulations.
The fundamental particles that make up our universe can be divided into two groups: particles called fermions, which are the building blocks of matter, and particles called bosons, which are field particles and tug on the matter particles.
In recent years, scientists have successfully developed quantum algorithms to compute systems made of fermions. But they've had a much tougher time doing the same for boson systems.
For the first time, Fermilab scientist Alexandru Macridin has found a way to model systems containing both fermions and bosons on general-purpose quantum computers, opening a door to realistic simulations of the subatomic realm. His work is part of the Fermilab quantum science program.
"The representation of bosons in quantum computing was never addressed very well in the literature before," Macridin said. "Our method worked, and better than we expected."
The relative obscurity of bosons in quantum-computation literature has partly to do with bosons themselves and partly with the way quantum-computing research has evolved.
Over the last decade, the development of quantum algorithms focused strongly on simulating purely fermionic systems, such as molecules in quantum chemistry.
"But in high-energy physics, we also have bosons, and high-energy physicists are particularly interested in the interactions between bosons and fermions," said Fermilab scientist Jim Amundson, a co-author on the Physical Review Letters paper. "So we took existing fermion models and extended them to include bosons, and we did that in a novel way."
The biggest barrier to modeling bosons related to the properties of a qubit—a quantum bit.
Mapping the states
A qubit has two states: one and zero.
Similarly, a fermion state has two distinct modes: occupied and unoccupied.
The qubit's two-state property means it can represent a fermion state pretty straightforwardly: One qubit state is assigned to "occupied," and the other, "unoccupied."
(You might remember something about the occupation of states from high school chemistry: An atom's electron orbitals can each be occupied by a maximum of one electron. So they're either occupied or not. Those orbitals, in turn, combine to form the electron shells that surround the nucleus.)
The one-to-one mapping between qubit state and fermion state makes it easy to determine the number of qubits you'll need to simulate a fermionic process. If you're dealing with a system of 40 fermion states, like a molecule with 40 orbitals, you'll need 40 qubits to represent it.
In a quantum simulation, a researcher sets up qubits to represent the initial state of, say, a molecular process. Then the qubits are manipulated according to an algorithm that reflects how that process evolves.
More complex processes need a greater number of qubits. As the number grows, so does the computing power needed to carry it out. But even with only a handful of qubits at one's disposal, researchers are able to tackle some interesting problems related to fermion processes.
"There's a well-developed theory for how to map fermions onto qubits," said Fermilab theorist Roni Harnik, a co-author of the paper.
Bosons, nature's force particles, are a different story. The business of mapping them gets complicated quickly. That's partly because, unlike the restricted, two-choice fermion state, boson states are highly accommodating.
Accommodating bosons
Since only one fermion can occupy a particular fermion quantum state, that state is either occupied or not—one or zero.
In contrast, a boson state can be variably occupied, accommodating one boson, a zillion bosons, or anything in between. That makes it tough to map bosons to qubits. With only two possible states, a single qubit cannot, by itself, represent a boson state.
With bosons, the question is not whether the qubit represents an occupied or unoccupied state, but rather, how many qubits are needed to represent the boson state.
"Scientists have come up with ways to encode bosons into qubits that would require a large number of qubits to give you accurate results," Amundson said.
A prohibitively large number, in many cases. By some methods, a useful simulation would need millions of qubits to faithfully model a boson process, like the transformation of a particle that ultimately produces a particle of light, which is a type of boson.
And that's just in representing the process's initial setup, let alone letting it evolve.
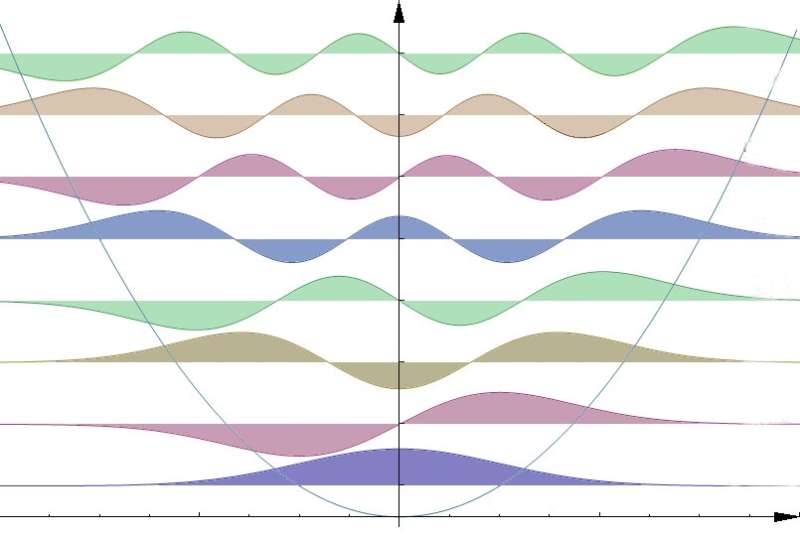
Macridin's solution was to recast the boson system as something else, something very familiar to physicists—a harmonic oscillator.
Harmonic oscillators are everywhere in nature, from the subatomic to the astronomical scales. The vibration of molecules, the pulse of current through a circuit, the up-and-down bob of a loaded spring, the motion of a planet around a star—all are harmonic oscillators. Even bosonic particles, like those Macridin looked to simulate, can be treated like tiny harmonic oscillators. Thanks to their ubiquity, harmonic oscillators are well-understood and can be modeled precisely.
With a background in condensed-matter physics—the study of nature a couple of notches up from its particle foundation—Macridin was familiar with modeling harmonic oscillators in crystals. He found a way to represent a harmonic oscillator on a quantum computer, mapping such systems to qubits with exceptional precision and enabling the precise simulation of bosons on quantum computers.
And at a low qubit cost: Representing a discrete harmonic oscillator on a quantum computer requires only a few qubits, even if the oscillator represents a large number of bosons.
"Our method requires a relatively small number of qubits for boson states—exponentially smaller than what was proposed by other groups before," Macridin said. "For other methods to do the same thing, they would probably need orders of magnitude larger number of qubits."
Macridin estimates that six qubits per boson state is enough to explore interesting physics problems.
Simulation success
As a trial of Macridin's mapping method, the Fermilab group first tapped into quantum field theory, a branch of physics that focuses on modeling subatomic structures. They successfully modeled the interaction of electrons in a crystal with the vibrations of the atoms that form the crystal. The 'unit' of that vibration is a boson called a phonon.
Using a quantum simulator at nearby Argonne National Laboratory, they modeled the electron-phonon system and—voila!—they showed they could calculate, with high accuracy, the system's properties using only about 20 qubits. The simulator is a classical computer that simulates how a quantum computer, up to 35 qubits, works. Argonne researchers leverage the simulator and their expertise in scalable algorithms to explore the potential impact of quantum computing in key areas such as quantum chemistry and quantum materials.
"We showed that the technique worked," Harnik said.
They further showed that, by representing bosons as harmonic oscillators, one could efficiently and accurately describe systems involving fermion-boson interactions.
"It turned out to be a good fit," Amundson said.
"I'd started with one idea, and it didn't work, so then I changed the representation of the bosons," Macridin said. "And it worked well. It makes the simulation of fermion-boson systems feasible for near-term quantum computers."
Universal application
The Fermilab group's simulation is not the first time scientists have modeled bosons in quantum computers. But in the other cases, scientists used hardware specifically designed to simulate bosons, so the simulated evolution of a boson system would happen naturally, so to speak, on those special computers.
The Fermilab group's approach is the first that can be applied efficiently in a general-purpose, digital quantum computer, also called a universal quantum computer.
The next step for Macridin, Amundson and other particle physicists at Fermilab is to use their method on problems in high-energy physics.
"In nature, fermion-boson interactions are fundamental. They appear everywhere," Macridin said. "Now we can extend our algorithm to various theories in our field."
Their achievement extends beyond particle physics. Amundson says their group has heard from materials scientists who think the work could be useful in solving real-world problems in the foreseeable future.
"We introduced bosons in a new way that requires fewer resources," Amundson said. "It really opens up a whole new class of quantum simulations."
More information: Alexandru Macridin et al. Electron-Phonon Systems on a Universal Quantum Computer, Physical Review Letters (2018). DOI: 10.1103/PhysRevLett.121.110504
Journal information: Physical Review Letters
Provided by Fermi National Accelerator Laboratory