Surprising hidden order unites prime numbers and crystal-like materials

The seemingly random digits known as prime numbers are not nearly as scattershot as previously thought. A new analysis by Princeton University researchers has uncovered patterns in primes that are similar to those found in the positions of atoms inside certain crystal-like materials.
The researchers found a surprising similarity between the sequence of primes over long stretches of the number line and the pattern that results from shining X-rays on a material to reveal the inner arrangement of its atoms. The analysis could lead to predicting primes with high accuracy, said the researchers. The study was published Sept. 5 in the Journal of Statistical Mechanics: Theory and Experiment.
"There is much more order in prime numbers than ever previously discovered," said Salvatore Torquato, Princeton's Lewis Bernard Professor of Natural Sciences, professor of chemistry and the Princeton Institute for the Science and Technology of Materials. "We showed that the primes behave almost like a crystal or, more precisely, similar to a crystal-like material called a 'quasicrystal.'"
Primes are numbers that can only be divided by 1 and themselves. Very large primes are the building blocks of many cryptography systems. Primes appear to be sprinkled randomly along the number line, although mathematicians have discerned some order. The first few primes are 2, 3, 5, 7 and 11, becoming more sporadic higher in the number line.
Torquato and his colleagues have found that that, when considered over large swaths of the number line, prime numbers are more ordered than previously believed, falling within the class of patterns known as "hyperuniformity."
Hyperuniform materials have special order at large distances and include crystals, quasicrystals and special disordered systems. Hyperuniformity is found in the arrangement of cone cells in bird eyes, in certain rare meteorites, and in the large-scale structure of the universe.
The team showed that the order they found in the prime numbers maps to the pattern that results when X-rays interact with certain forms of matter. As a chemist, Torquato is familiar with X-ray crystallography, shining X-rays through a crystal's three-dimensional atomic lattice. With diamonds or other crystals, this will result in a predictable pattern of bright spots or peaks, known as Bragg peaks.
Compared to typical crystals, quasicrystals yield a distinct and more complex arrangement of Bragg peaks. The peaks in a typical crystal form at regular intervals with empty gaps between them. In quasicrystals, between any two selected Bragg peaks is another Bragg peak.
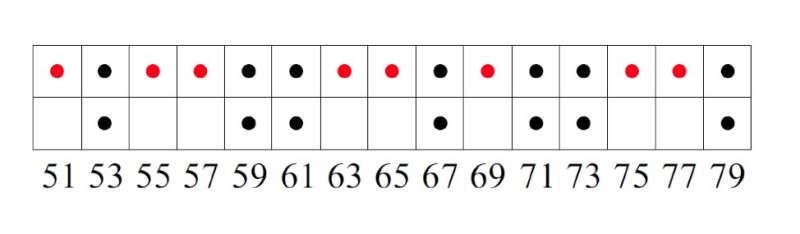
The pattern that Torquato and his colleagues discovered in the primes is similar to that of quasicrystals and another system called limit-periodic order, but it differs enough that the researchers call it "effectively limit-periodic" order. The prime numbers appear in "self-similar" groupings, meaning that between peaks of certain heights, there are groupings of smaller peaks, and so on.
The team discovered strong indications of such a pattern using computer simulations to see what would happen if prime numbers were treated like a string of atoms subjected to X-rays. In work published in the Journal of Physics A in February, the researchers reported finding a surprising pattern of Bragg-like peaks, indicating that the prime patterns were highly ordered.
The current study uses number theory to provide a theoretical foundation for those previous numerical experiments. The researchers realized that although primes appear random over short intervals, Torquato said, at sufficiently long stretches of the number line, sense can be made out of otherwise seemingly chaotic numbers.
"When you go to that distinguished limit, 'Boom!'" he said, snapping his fingers. "The ordered structure pops out."
Torquato co-authored the paper with Ge Zhang, who earned his doctorate in chemistry in 2017, and mathematics graduate student Matthew de Courcy-Ireland.
De Courcy-Ireland said that similar numerical patterns were described by the "circle method" developed nearly a century ago to find patterns in primes. "For me, what is interesting is taking these results that go back to 1922 and reformulating them in some way that gives you a new example, a system with a bunch of properties that is very interesting, and one that maybe could point the way to where you could look for more physical examples," he said.
The discovery may aid research in both mathematics and materials science. "Prime numbers have beautiful structural properties, including unexpected order, hyperuniformity and effective limit-periodic behavior," said Torquato. "The primes teach us about a completely new state of matter."
"What's fascinating about this paper is that it gives us a different perspective on the primes: instead of viewing them as numbers, we can view them as particles and try to map out their structure via X-ray diffraction," said Henry Cohn, a principal researcher at Microsoft Research who was not involved with the study. "It turns out to give us the same sort of information as traditional number-theoretic methods, and to tie in beautifully with previous work. It's a beautiful new perspective on this information, and it opens up new connections with materials science and scattering theory."
The study, "Uncovering multiscale order in the prime numbers via scattering," was published in the Journal of Statistical Mechanics: Theory and Experiment on Sept. 5.
More information: S Torquato et al. Uncovering multiscale order in the prime numbers via scattering, Journal of Statistical Mechanics: Theory and Experiment (2018). DOI: 10.1088/1742-5468/aad6be
Provided by Princeton University