April 10, 2018 report
Quantum simulator offers faster route for prime factorization
Factoring very large numbers into their prime "building blocks" is extremely difficult for classical computers, and this difficulty underlies the security of many cryptographic algorithms. While it's easy to factor the number 20 as the product of the primes 2 x 2 x 5, for example, factoring larger numbers becomes exponentially more difficult when using classical factoring algorithms.
In a new paper published in Physical Review A, physicists Jose Luis Rosales and Vicente Martin have developed a method that may make it much easier to factor very large numbers that are known to have exactly two prime factors. The new method determines the probability that any prime number is one of the two prime factors of a given number. After determining these odds, the most likely prime factor candidates can be tested first, allowing for the prime factors to be identified much more quickly than before.
"The theory shows not only where the primes are located, but also the probability for a prime to be a factor of a given number," Rosales told Phys.org. "Of course, this has implications in cryptography because [the cryptosystem] RSA ignores this regularity."
One of the interesting things about the new method is that it doesn't use any kind of computer, either classical or quantum. Instead it involves a physical quantum system—a "quantum simulator"—that, when encoded with the number to factor, exhibits a probability distribution of energy values that is equivalent to the probability distribution of the prime factor candidates of the encoded number.
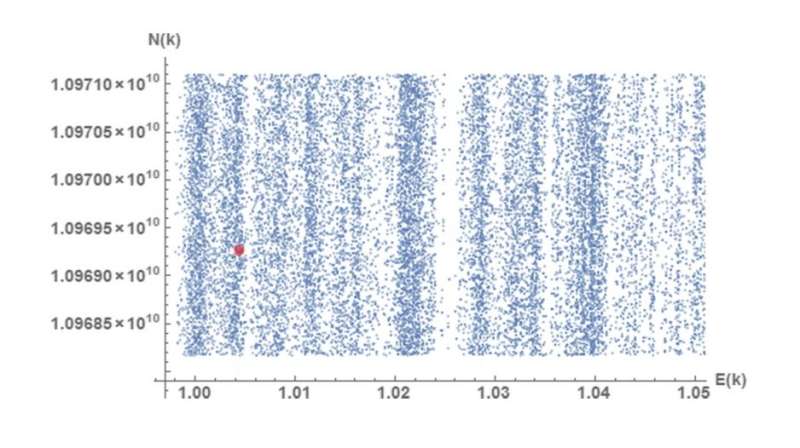
"Our aim is to develop a new quantum theory of the factorization problem using a quantum simulator," Rosales said. "Our approach has discovered a property with no classical analogy in number theory. Every pair of primes that solve the problem re-arrange themselves to form a regular pattern: the band spectrum of the quantum simulator."
The general idea behind the quantum simulator is something called the "factorization ensemble," which the researchers introduced previously. It is based on the idea that the primes are ordered from least to greatest (for example, 2 is the first prime, 3 is the second prime, and 101 is the 26th prime). It's also possible to take the square root of any number, and then compare the result to the closest prime. For example, the square root of 27 is a little more than 5, which is the third prime. By the definition of a factorization ensemble, this means that 27 belongs to the factorization ensemble of 3.
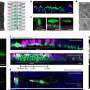
The physicists then showed that they could transform the factorization ensemble function into a function from quantum physics (the inverted harmonic-oscillator function). After many more steps, they eventually showed that the predicted energy spectrum of a quantum system corresponds to the distribution of primes in the factorization ensemble of a number. From this information, the researchers can determine the probability that a prime is a factor of that number. To test the validity of their method, the physicists tested certain numbers and compared their results to the actual distributions obtained using prime number tables, and found very similar distributions.
The physicists theoretically demonstrated that the proposed quantum simulator can factor numbers that are many orders of magnitude larger than those that have been factored with quantum computers. In their paper, they report the results of using their method to determine the probability distribution of the prime factors of a number with 24 digits. Further, the method does this with far fewer resources than required by classical factoring algorithms.
"In quantum theory, the algorithmic complexity is only polynomial with the number of bits of the number to factorize," Rosales said. "As a matter of fact, our first results seem to confirm that the simulator requires only (log√N)3 quantum states to reproduce its spectrum of energies, a very encouraging result."
One final point of interest is that the new method has strong connections to the Riemann hypothesis, which, if true, would suggest that the prime numbers are distributed in a predictable way—in the same way as the distribution of the zeros of the Riemann-zeta function. Proving (or disproving) the Riemann hypothesis is one of the greatest unsolved problems in mathematics, and one of the Clay Mathematics Institute's Millennium Prize Problems.
"The primes should behave as quantum numbers if Hilbert-Polya's conjecture applies," Rosales said, referring to the long-standing approach to proving the Riemann hypothesis.
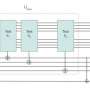
Going forward, the researchers are currently working on the experimental implementation of the quantum simulator by using two entangled particles in a Penning trap.
"The fully quantum treatment of the simulator would require quantum optical analysis of the interactions of photons with two (or more) entangled ions in a Penning trap," Rosales said. "This part of the program is yet in development. The aim is to build a quantum factoring simulator experimentally. If successfully implemented, numbers many orders of magnitude bigger than those available for its quantum processing using Shor's algorithm will be factorized and, as a by-product, the Hilbert-Polya conjecture will be tested experimentally."
More information: Jose Luis Rosales and Vicente Martin. "Quantum simulation of the integer factorization problem: Bell states in a Penning trap." Physical Review A. DOI: 10.1103/PhysRevA.97.032325. Also at: arXiv:1704.03174 [quant-ph]
Journal information: Physical Review A
© 2018 Phys.org