November 28, 2014 report
New largest number factored on a quantum device is 56,153
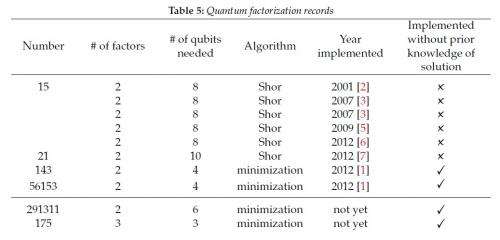
(Phys.org)—Researchers have set a new record for the quantum factorization of the largest number to date, 56,153, smashing the previous record of 143 that was set in 2012. They have shown that the exact same room-temperature nuclear magnetic resonance (NMR) experiment used to factor 143 can actually factor an entire class of numbers, although this was not known until now. Because this computation, which is based on a minimization algorithm involving 4 qubits, does not require prior knowledge of the answer, it outperforms all implementations of Shor's algorithm to date, which do require prior knowledge of the answer. Expanding on this method, the researchers also theoretically show how the same minimization algorithm can be used to factor even larger numbers, such as 291,311, with only 6 qubits.
On top of this, in the same paper the researchers demonstrated the first quantum factorization of a "triprime," which is the product of three prime numbers. Here, the researchers used a 3-qubit factorization method to factor the triprime 175, which has the factors 5, 5, and 7.
Nike Dattani at Kyoto University and Oxford University, along with Nathaniel Bryans at Microsoft (now at the University of Calgary), have described their results in a recent paper posted at arXiv.org.
As the researchers explain, the minimization algorithm used to achieve these results has been steadily improving since its introduction in 2001, especially in comparison with Shor's algorithm, which was introduced in 1994. The largest number factored by Shor's algorithm to date is only 21, and even this factorization relied on prior knowledge of the answer to the problem being solved in the first place.
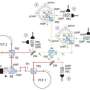
The minimization algorithm is different than Shor's algorithm in that it turns the factorization problem into an optimization problem, and then uses a quantum device to solve for the minimum values, which encode the factors. (The minimum values are not themselves the factors. For example, if the minimum values found are p1 = 0 and p2 = 1, and one factor is p = 1, p2, p1, 1 in binary, then p = 1101, which corresponds to 13 as one of the factors.)
This computation is how, in 2012, Xu, et al., factored the number 143 (11 x 13). It's also how Dattani and Bryans factor several other numbers in the new paper, the largest of which is 56,153 (241 x 233).
"We're still a far way from outperforming classical computers," Dattani told Phys.org. "The highest RSA number factored on a classical computer was RSA-768, which has 768 bits, and took two years to compute (from 2007 to 2009)."
RSA numbers are a set of large "semiprimes"—numbers with exactly two prime factors. RSA numbers are particularly special due to the difficulty in factoring them. For this reason, they are used by governments, militaries, and banks to keep financial information secure.
"56,153 only has 16 bits," Dattani explained. "However, that's twice the number of bits in the largest number factored using Shor's algorithm to date; and while factoring 56,153 via minimization only required 4 qubits, factoring 21 with Shor's algorithm requires 10."
Although the minimization algorithm is a true quantum method, the equations can also be quickly and easily solved by a classical computer because they contain only four variables, and therefore solving them involves only 24 = 16 queries.
In order for quantum computers to provide real, practical advantages over classical computers, the equations must have many more than four variables. For example, a case in which the equations have 512 variables, which is the number of qubits in the D-Wave Two quantum computer, would require 2512 queries. Using a brute force "guess and check" strategy, a classical computer that makes a trillion queries per second would take 10123 times the age of the universe to factor such a number.
This issue raises the question of how to tell which large numbers will reduce to a set of equations with a large number of variables, as these are the numbers that would benefit from quantum treatment. Here, Dattani and Bryans have noticed certain patterns that may help identify these numbers when they are semiprime.
Specifically, they found that the semiprimes that would gain the most benefit from the power of a quantum computer would have factors that differ at a large number of bit positions (for example, 110101 and 101010 differ by five of six bit positions). The factors of 291,311 (557 x 523) differ at a large number of bit positions, and the researchers demonstrated how to factor this number using the minimization technique with 6 qubits. (Unlike the factorization of 56,153, the factorization of 291,311 has not yet been experimentally implemented, so it doesn't count as a new record yet.)
Until now, semiprimes have been the only numbers for which quantum factorization has been successfully demonstrated. But Dattani and Bryans address this issue as well, and demonstrate the quantum factorization of the triprime 175 with three qubits (which also has not been experimentally implemented).
"Shor's algorithm can in theory factor large numbers with fewer quantum circuit operations than the number of classical operations required for factoring on a classical computer," Dattani said. "However, performing quantum circuit operations is mighty hard, so it's not clear which type of computer would win the race to factor, for example, RSA-896. The alternative to Shor's algorithm, that we discussed, is still a quantum computation, but it does not rely on quantum circuit operations. We want to work out whether this circuitless quantum computation can factor something that a classical computer cannot do."
More information: Nikesh S. Dattani and Nathaniel Bryans. "Quantum factorization of 56153 with only 4 qubits." arXiv:1411.6758 [quant-ph]
© 2014 Phys.org