New tools reveal prelude to chaos

Picture a herd of sheep or cattle emerging from a shed or barn to graze a field. They head straight out of their digs to the pleasure of the pasture pretty much as one entity, but as the land opens up and the "grass gets greener" they disperse randomly in a motion that has neither rhyme nor reason. Individual animals depart at different angles from the herd and then at different angles from their original departure and so on until "the cows come home."
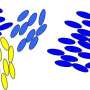
In physics, this movement that starts off on the straight-and-narrow (ballistic) and is correlated and then dissolves into randomness (diffusive), uncorrelated, is called a ballistic-to-diffusive transition. Researchers in a number of fields call this motion a "random walk," also known as diffusive motion, a universal phenomenon that occurs in both physical (atomic-cluster diffusion, nanoparticle scattering and bacterial migration) and nonphysical (animal foraging, stock price fluctuations and "viral" internet postings) systems.
Engineers at Washington University in St. Louis have developed mathematical tools that send that shot across the bow—they determine when randomness emerges in any stochastic (random) system, answering a long-standing question: When does randomness set in during a random walk?
Led by Rajan K. Chakrabarty, assistant professor of energy, environmental and chemical engineering, the researchers have provided 11 equations that they applied to directional statistics. The resulting tools mathematically describe the kinetics in a system right before it dissolves into randomness as well as the walker's turning angle distribution. The tools have the potential to be useful in predicting the onset of chaos in everything from nanoparticles to checking accounts.
The research was published in a recent issue of Physical Review E.
"We hope that we have shown a new starting point to investigate randomness," Chakrabarty said. "We are trying to describe an effect as exactly as possible irrespective of the cause. Now we can see the prelude to chaos so that people might have the ability to intervene and reverse a trend. From this point on, we hope to apply this mathematics to various systems and see how general our predictions are and what needs to be tweaked."
Chakrabarty, whose doctorate is in chemical physics, said that physicists normally solve problems by mathematically describing a cause and effect and marrying the two for a solution. But this new tool cares nothing about the cause, only about mathematically capturing the effect.
Chakrabarty's graduate student, Pai Liu, produced eight of the 11 equations in the paper.
"The research started with the goal of establishing a mathematical relationship to the behavior of chaotic motion," Liu said. "The equations have a significant time component. We think that we've come up with mathematical formulations, general in nature, that can be applied to any random motion to describe their transport properties and find the critical time step at which the transition from ballistic to diffusive takes place."
More information: Pai Liu et al, Establishing the kinetics of ballistic-to-diffusive transition using directional statistics, Physical Review E (2018). DOI: 10.1103/PhysRevE.97.042102
Journal information: Physical Review E
Provided by Washington University in St. Louis