Researchers validate several fluctuation theorems for first time

Researchers at Purdue University have performed the first experimental tests of several fundamental theorems in thermodynamics, verifying the relationship between them and providing a better understanding of how nanoparticles behave under fluctuation.
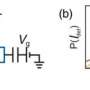
As a system gets smaller, fluctuations away from equilibrium begin to dominate its behavior. This makes the data from experiments in small systems, such as biological molecular motors and nanoscale magnets, messy and difficult to make sense of. Fluctuation theorems help researchers make sense of the fluctuations in these systems.
Fluctuation theorems are refinements of the second law of thermodynamics, which states that all kinds of energy in the material world disperses if it is not hindered from doing so.
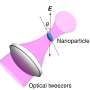
A team of researchers from Purdue and Peking University, led by Tongcang Li, assistant professor of physics and astronomy at Purdue, tested the differential fluctuation theorem for work production and several other theorems. They levitated a nanoparticle in a vacuum chamber with a laser, using a tiny optical tweezer to measure instantaneous position and velocity. This mechanism allows them to trap the nanoparticle in air continuously for weeks or months and acquire large sets of data.
The research was published in Physical Review Letters.
More information: Thai M. Hoang et al. Experimental Test of the Differential Fluctuation Theorem and a Generalized Jarzynski Equality for Arbitrary Initial States, Physical Review Letters (2018). DOI: 10.1103/PhysRevLett.120.080602
Journal information: Physical Review Letters
Provided by Purdue University