Recurrences in an isolated quantum many-body system
It is one of the most astonishing results of physics—when a complex system is left alone, it will return to its initial state with almost perfect precision. Gas particles, for example, chaotically swirling around in a container, will return almost exactly to their starting positions after some time. The Poincaré Recurrence Theorem is the foundation of modern chaos theory. For decades, scientists have investigated how this theorem can be applied to the world of quantum physics. Now, researchers at TU Wien (Vienna) have successfully demonstrated a kind of Poincaré recurrence in a multi-particle quantum system. The results have been published in the journal Science.
At the end of the 19th century, the French scientist Henri Poincaré studied systems that cannot be fully analysed with perfect precision—for example, solar systems consisting of many planets and asteroids, or gas particles that keep bumping into each other. His surprising result: Every state that is physically possible will be occupied by the system at some point—at least to a very good degree of approximation. If we just wait long enough, at some point all planets will form a straight line, just by coincidence. The gas particles in a box will create interesting patterns, or go back to the state in which they were when the experiment started.
A similar theorem can be proved for quantum systems. There, however, completely different rules apply: "In quantum physics, we have to come up with a completely new way of addressing this problem," says Professor Jörg Schmiedmayer from the Institute for Atomic and Subatomic Physics at TU Wien. "For very fundamental reasons, the state of a large quantum system, consisting of many particles, can never be perfectly measured. Apart from that, the particles cannot be seen as independent objects, we have to take into account that they are quantum mechanically entangled."

There have been attempts to demonstrate the effect of "Poincaré recurrence" in quantum systems, but until now this has only been possible with a very small number of particles, whose state was measured as precisely as possible. This is extremely complicated and the time it takes the system to return to its original state increases dramatically with the number of particles. Jörg Schmiedmayers team at TU Wien, however, chose a different approach: "We are not so much interested in the complete inner state of the system, which cannot be measured anyway," says Bernhard Rauer, first author of the publication. "Instead we want to ask: which quantities can we observe, that tell us something interesting about the system as a whole? And are there times at which these collective quantities return to their initial value?"
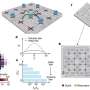
The team studied the behaviour of an ultracold gas, consisting of thousands of atoms, which is kept in place by electromagnetic fields on a chip. "There are several different quantities describing the characteristics of such a quantum gas—for example coherence lengths in the gas and correlation functions between different points in space. These parameters tell us, how closely the particles are linked by quantum mechanical effects," says Sebastian Erne, who was responsible for the theoretical calculations necessary for the project. "Our everyday intuition is not used to dealing with these quantities, but for a quantum systems, they are crucial."
Recurrence Discovered—in Collective Quantities
By measuring such quantities, which do not refer to single particles, but characterize the system as a whole, it was indeed possible to observe the long-sought quantum recurrence. And not only that: "With our atom chip, we can even influence the time it takes the system to return to one particular state," says Jörg Schmiedmayer. "By measuring this kind of recurrence, we learn a lot about the collective dynamics of the atoms—for example about the speed of sound in the gas or about scattering phenomena of density waves."
The old question, whether quantum systems show recurrences, can finally be answered: Yes, they do—but the concept of recurrence has to be slightly redefined. Instead of trying to map out the complete inner quantum state of a system, which cannot be measured anyway, it makes more sense to concentrate on quantities which can be measured in quantum experiments. These quantities can be observed to drift away from their initial value—and to return to their initial state eventually.
More information: Bernhard Rauer et al, Recurrences in an isolated quantum many-body system, Science (2018). DOI: 10.1126/science.aan7938
Journal information: Science
Provided by Vienna University of Technology