Leaving flatland – quantum Hall physics in 4-D

In literature, the potential existence of extra dimensions was discussed in Edwin Abbott's satirical novel "Flatland: A Romance of Many Dimensions" (1884), portraying the Victorian society in 19th century England as a hierarchical two-dimensional world, incapable of realizing its narrow-mindedness due to its lower-dimensional nature.
In physics, on the other hand, the possibility that our universe comprises more than three spatial dimensions was first proposed in the wake of Albert Einstein's theory of general relativity in the 1920s. Modern string theory – trying to reconcile Einstein's ideas with the laws of quantum mechanics – even postulates up to 10 dimensions.
In a completely different context, an international team of researchers led by Professor Immanuel Bloch (LMU/MPQ) and Professor Oded Zilberberg (ETH Zürich) has now demonstrated a way to observe physical phenomena proposed to exist in higher-dimensional systems in analogous real-world experiments. Using ultracold atoms trapped in a periodically modulated two-dimensional superlattice potential, the scientists could observe a dynamical version of a novel type of quantum Hall effect that is predicted to occur in four-dimensional systems.
The Hall effect occurs when charged particles move in a two-dimensional plane in the presence of a magnetic field. The magnetic field generates a Lorentz force, which deflects the particles in the direction orthogonal to their motion. This manifests in the appearance of a transverse Hall voltage. In 1980, Klaus von Klitzing made the remarkable discovery that at low temperatures and very strong magnetic fields this voltage can only take certain quantized values.
Moreover, these values are identical irrespective of the specific properties of the experimental sample. This astonishing fact was later shown to be related to the topology of the quantum mechanical wave functions describing the behaviour of electrons at such low energies – a seminal work for which David Thouless was awarded the Nobel prize in physics in 2016.
An important prerequisite for the quantum Hall effect turned out to be the two-dimensional geometry of the sample. It can be proven that in general such a phenomenon cannot take place in three-dimensional systems – as exemplified by the fact that the direction transverse to the velocity of the particles is not defined uniquely in three dimensions. Thus, it was believed that this effect is special to two dimensions.
Yet, 20 years after the initial discovery theoretical physicists postulated that a similar effect could also take place in four-dimensional systems, for which even more remarkable properties including a novel non-linear Hall current were predicted. For a long time, however, this proposal was mostly regarded as a mathematical curiosity – out of reach for actual experiments – despite its far-reaching implications. For example, both topological insulators and Weyl semimetals, two of the most prominent discoveries in condensed matter physics in recent years, can be derived from 4-D quantum Hall models.
In 2013, Oded Zilberberg and collaborators realized that key signatures of the 4-D quantum Hall effect should also be visible in special time-dependent systems in two dimensions, so-called topological charge pumps, which constitute a dynamical version of the higher-dimensional model. This insight generalized an idea, which also goes back to David Thouless. In 1983, Thouless showed that a quantized transport of particles can be generated by periodically modulating a 1D system and that this response is mathematically equivalent to the 2-D quantum Hall effect. Consequently, by combining two such systems in orthogonal directions, it should be possible to observe the non-linear Hall current predicted in 4-D.
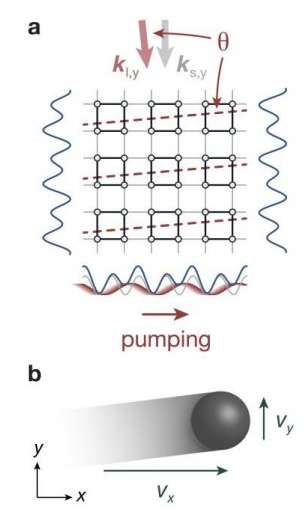
This has now been achieved by the group of Immanuel Bloch. At first a cloud of atoms is cooled down close to absolute zero and placed in a 2-D optical lattice. Such an optical lattice is created by interference of retro-reflected laser beams of a certain wavelength along two orthogonal directions. The resulting potential resembles an egg-carton-like "crystal of light", in which the atoms can move. By adding another laser beam with a different wavelength in each direction, a so-called superlattice is created.
The researchers could implement the proposed 2-D topological charge pump by introducing a constant tiny angle between the beams of different wavelength along one axis while at the same time dynamically changing the shape of the potential in the orthogonal direction by slightly shifting the wavelength of the additional laser beam.
When modulating the potential in time, the atoms predominantly move in the direction of the modulation and do so in a quantized way – the linear (i.e. 1D) response corresponding to the 2-D quantum Hall effect as predicted by Thouless. But in addition to this, the Munich team also observed a slight drift in the transverse direction, even though the lattice potential in this direction remains static throughout the experiment. This transverse motion is the equivalent of the non-linear Hall response – the essential feature of the 4-D Hall effect. By carefully monitoring and analyzing at which positions in the superlattice the atoms are located during this process, the scientists could furthermore demonstrate that this motion is quantized, thereby revealing the quantum nature of the Hall effect in 4-D.
The results have now been published in the journal Nature ("Exploring 4-D quantum Hall physics with a 2-D topological charge pump") together with complementary work by an American research team, which used photonic structures to study the intricate boundary phenomena that accompany this motion as a result of the 4-D quantum Hall effect.
Together, these papers provide the first experimental glimpse into the physics of higher-dimensional quantum Hall systems, which offer a number of fascinating future prospects. These include fundamental questions for our understanding of the universe like the interplay of quantum correlations and dimensionality, the generation of cosmic magnetic fields and quantum gravity, for which 4-D quantum Hall systems have been proposed as toy models.
More information: Michael Lohse et al. Exploring 4-D quantum Hall physics with a 2-D topological charge pump, Nature (2018). DOI: 10.1038/nature25000
Oded Zilberberg et al. Photonic topological boundary pumping as a probe of 4D quantum Hall physics, Nature (2018). DOI: 10.1038/nature25011
Journal information: Nature
Provided by Max Planck Society