Physics may bring faster solutions for tough computational problems

A well-known computational problem seeks to find the most efficient route for a traveling salesman to visit clients in a number of cities. Seemingly simple, it's actually surprisingly complex and much studied, with implications in fields as wide-ranging as manufacturing and air-traffic control.
Researchers from the University of Central Florida and Boston University have developed a novel approach to solve such difficult computational problems more quickly. As reported May 12 in Nature Communications, they've discovered a way of applying statistical mechanics, a branch of physics, to create more efficient algorithms that can run on traditional computers or a new type of quantum computational machine, said Professor Eduardo Mucciolo, chair of the Department of Physics in UCF's College of Sciences.
Statistical mechanics was developed to study solids, gasses and liquids at macroscopic scales, but is now used to describe a variety of complex states of matter, from magnetism to superconductivity. Methods derived from statistical mechanics have also been applied to understand traffic patterns, the behavior of networks of neurons, sand avalanches and stock market fluctuations.
There already are successful algorithms based on statistical mechanics that are used to solve computational problems. Such algorithms map problems onto a model of binary variables on the nodes of a graph, and the solution is encoded on the configuration of the model with the lowest energy. By building the model into hardware or a computer simulation, researchers can cool the system until it reaches its lowest energy, revealing the solution.
"The problem with this approach is that often one needs to get through phase transitions similar to those found when going from a liquid to a glass phase, where many competing configurations with low energy exist," Mucciolo said. "Such phase transitions slow down the cooling process to a crawl, rendering the method useless."
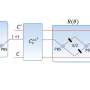
Mucciolo and fellow physicists Claudio Chamon and Andrei Ruckenstein of BU overcame this hurdle by mapping the original computational problem onto an elegant statistical model without phase transitions, which they called the vertex model. The model is defined on a two-dimensional lattice and each vertex corresponds to a reversible logic gate connected to four neighbors. Input and output data sit at the boundaries of the lattice. The use of reversible logic gates and the regularity of the lattice were crucial ingredients in avoiding the phase-transition snag, Mucciolo said.
"Our method basically runs things in reverse so we can solve these very hard problems," Mucciolo said. "We assign to each of these logic gates an energy. We configured it in such a way that every time these logic gates are satisfied, the energy is very low - therefore, when everything is satisfied, the overall energy of the system should be very low."
Chamon, a professor of physics at BU and the team leader, said the research represents a new way of thinking about the problem.
"This model exhibits no bulk thermodynamic-phase transition, so one of the obstructions for reaching solutions present in previous models was eliminated," he said.
The vertex model may help solve complex problems in machine learning, circuit optimization, and other major computational challenges. The researchers are also exploring whether the model can be applied to the factoring of semi-primes, numbers that are the product of two prime numbers. The difficulty of performing this operation with very large semi-primes underlies modern cryptography and has offered a key rationale for the creation of large-scale quantum computers.
Moreover, the model can be generalized to add another path toward the solution of complex classical computational problems by taking advantage of quantum mechanical parallelism—the fact that, according to quantum mechanics, a system can be in many classical states at the same time.
"Our paper also presents a natural framework for programming special-purpose computational devices, such as D-Wave Systems machines, that use quantum mechanics to speed up the time to solution of classical computational problems," said Ruckenstein.
Zhi-Cheng Yang, a graduate student in physics at BU, is also a co-author on the paper. The universities have applied for a patent on aspects of the vertex model.
More information: C. Chamon et al, Quantum vertex model for reversible classical computing, Nature Communications (2017). DOI: 10.1038/ncomms15303
Journal information: Nature Communications
Provided by University of Central Florida