Natural systems show nonlocal correlations

Classical correlations are part of our everyday life. For instance, if one always puts on a pair of socks of the same color and shape, looking at the color or shape of one sock determines the color or shape of its pair. Even more, by observing the color and shape of one sock and we can simultaneously know the color and shape of the other one.
In the quantum realm, Heisenberg's uncertainty principle states that accurately measuring a pair of properties of an atom puts a limit to the precision of measurement you can obtain on the same properties of another atom. Therefore, if the socks are said to be entangled, observing the color of one sock would allow us to predict the color of the other. However, if we also observe the shape of the sock, this would "disturb" the color, making it completely unpredictable to a certain extent. This weird "synchronization" between particles is defined as quantum entanglement, and is one of the intrinsic features of the quantum world.
In nature, there exists a much stranger form of so-called nonlocal correlations, which are manifested by some entangled states between atomic particles. By making the minimal assumptions that properties of objects (shape/color) exist regardless of our knowledge of them, and that information cannot propagate instantaneously, one finds that quantum physics can generate correlations that are incompatible with these two apparently reasonable principles.
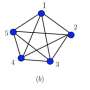
Although extremely fascinating to study, these nonlocal correlations are very hard to characterize in systems composed of many particles for three reasons. First, classical correlations are mathematically very complex to study; second, quantum many-body states are very complex to describe due to the exponential growth of their described states; and, third, currently available experimental techniques are rather limited, constraining the measurements that can be performed in the laboratory. In order to explore the role of nonlocal correlations in many-body quantum systems, one thus has to address these three problems at the same time.
In a recent paper published in Physical Review X, a team of scientists from MPQ in Munich, ICFO in Barcelona, University of Innsbruck and the Center for Theoretical Physics of the Polish Academy of Sciences have proposed a simple test to study nonlocal correlations in quantum many-body systems. They have studied whether nonlocal correlations appear in natural systems as ground states of some spin Hamiltonians, such as electrons (described by their spin degree of freedom) in a system of one spatial dimension. By combining numerical and analytical results, they have shown that some Hamiltonians that have been studied by physicists for some decades have a state of minimal energy that can display nonlocal correlations.
As the first author, Jordi Tura, has commented, "We provide a set of tools to study a problem that has always been complicated on its own. The techniques we developed are much simpler than previous ones. If you wanted to implement them in the lab, you would just need to ensure that the system is prepared in a state of sufficiently low energy."
The results sheds some light onto this fascinating problem, hopefully sparking further progress in our understanding of nonlocality in quantum many-body systems.
More information: J. Tura, G. De las Cuevas, R. Augusiak, M. Lewenstein, A. Acín, J. I. Cirac, Energy as a detector of nonlocality of many-body spin systems, Phys. Rev. X, 7, 021005 (2017)
Journal information: Physical Review X
Provided by ICFO