March 16, 2017 feature
Quantum shortcuts cannot bypass the laws of thermodynamics

(Phys.org)—Over the past several years, physicists have developed quantum shortcuts that speed up the operation of quantum systems. Surprisingly, some of these shortcuts theoretically appear to enable systems to operate nearly instantaneously while using no extra energy—a clear violation of the second law of thermodynamics. Although physicists have known that something is amiss, so far the solution to this predicament has been unclear.
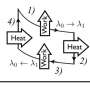
Now in a new study, physicists have shown that quantum shortcuts are subject to a trade-off between speed and cost, so that the faster a quantum system evolves, the higher the energetic cost of implementing the shortcut. In accordance with the laws of thermodynamics, an infinitely fast speed would be impossible since it would require an infinite amount of energy.
The physicists, Steve Campbell at Queen's University Belfast in the UK and the University of Milan in Italy, along with Sebastian Deffner at the University of Maryland Baltimore County in the US, have published a paper on the trade-off between cost and speed in quantum shortcuts in a recent issue of Physical Review Letters.
"Some recently proposed methods to control quantum systems, called shortcuts to adiabaticity (STA), appear to be energetically for free, and even more concerning there was nothing to say they couldn't be achieved in vanishingly small times," Campbell told Phys.org. "That something wasn't quite right led us to more explicitly consider what happens when these techniques are applied."
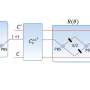
To do this, the scientists applied the quantum speed limit—a fundamental upper bound on the speed at which a quantum system can operate, which arises due to the Heisenberg uncertainty principle. Since the quantum speed limit is a consequence of this fundamental principle, it must apply to all STAs, and so it should prohibit them from operating in arbitrarily short times.
"By calculating the quantum speed limit, we showed that the faster you want to manipulate a system using an STA, the higher the thermodynamic cost," Campbell. "Moreover, instantaneous manipulation is impossible since it would require an infinite energy to be put in."
As the scientists explained, the results are not particularly surprising, just something that took time to figure out.
"I believe this is another case of 'if something seems too good to be true, it typically is,'" Deffner said. "There was probably a general sense in the community that one will have to quantify the cost. We were just the first to work it out."
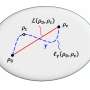
To demonstrate the usefulness of this trade-off, the physicists applied it to two practical systems. The first is harmonic oscillators, which have a wide range of uses, including in tests of quantum thermodynamics. The second is the Landau-Zener model, which has applications in adiabatic quantum computing, as used in the D-Wave machine.
In both models, the tradeoff places practical limits on the ultimate speed-up of these systems offered by STAs. The scientists expect that these limitations will help guide the design and implementation of these and other quantum systems in the future.
"We would also like to look into the other techniques for STA that have been developed, and see whether we can find similar trade-offs," Deffner said. "Another important route will be to generalize our work to non-standard quantum mechanics, such as Dirac materials and nonlinear systems."
More information:
Steve Campbell and Sebastian Deffner. "Trade-Off Between Speed and Cost in Shortcuts to Adiabaticity." Physical Review Letters. DOI: 10.1103/PhysRevLett.118.100601
Also at arXiv:1609.04662 [quant-ph]
Journal information: Physical Review Letters
© 2017 Phys.org