Busting myths about the metric system

This week is the 41st anniversary of the Metric Conversion Act, which was signed on December 23, 1975, by President Gerald R. Ford. Normally, we celebrate by sharing metric education resources, but this year I want to use the occasion to dispel some common misconceptions about the U.S. relationship with the metric system.

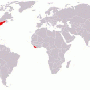
You've probably heard that the United States, Liberia and Burma (aka Myanmar) are the only countries that don't use the metric system (International System of Units or SI). You may have even seen a map that has been incriminatingly illustrated to show how they are out of step with the rest of the world.

It's a compelling story and often repeated, but you might be surprised to learn that it's simply untrue!

While it's true that metric use is mandatory in some countries and voluntary in others, all countries have recognized and adopted the SI, including the United States.

Dr. Russ Rowlett at the University of North Carolina at Chapel Hill emphasizes on his website that becoming metric is not a one-time event but a process that happens over time. Every international economy is positioned somewhere along a continuum moving toward increased SI use. There are still countries that are amending their national laws to adopt mandatory metric policy and others pursuing voluntary metrication.

The Unites States was one of the original countries to sign the Treaty of the Meter in 1875, which is now celebrated annually on May 20, World Metrology Day. It's been legal to use the metric system since 1866, and metric became the preferred system of weights and measures for U.S. trade and commerce in 1988.

It's impossible to avoid using the metric system in the United States. All our measurement units, including U.S. customary units you're familiar with (feet, pounds, gallons, Fahrenheit, etc.), are defined in terms of the SI—and have been since 1893! The SI's influence is pervasive and felt even if most people don't know it. I envision U.S. metric practice like a huge iceberg. Above the water's surface, U.S. customary units appear to still be in full effect. In actuality, below the water's surface we find that all measurements are dependent on the SI, linked through an unbroken chain of traceable measurements.

Although U.S. customary units are still seen alongside metric units on product labels and merchandise literature, it's common for the goods themselves to be made using SI-based manufacturing processes. Why? While some businesses are concerned that consumers expect to see customary units on the package, when it comes to manufacturing processes, they are under constant pressure to stay competitive. Adopting the latest science and technology, developed using metric design practices, enables innovation. In addition, many industries extensively use international supply lines to develop, manufacture, and sell their products around the world.

I'm the coordinator of NIST's Metric Program. Because of my passion for all things metric, I encourage companies to investigate adopting metric practices whenever possible and show them how doing so can make a strategic economic impact for their organization. Changes in technology and extremely competitive domestic and global marketplaces can compel businesses with little previous experience to explore metric use. Many have found that going metric pays off, resulting in a competitive advantage.

If your business is considering making the switch to metric, I would encourage you to conduct small beta tests to explore how your customers react. Research can help ensure decisions aren't based on out-of-date information or preconceived notions. You might be pleasantly surprised by how quickly customers adapt—and how using metric benefits the bottom line.

And as always, if you need advice, be sure to give NIST a call; we're here to help!

Going Metric Pays Off

During the recent recession, lumber companies located in the U.S. Northwest saw their U.S. customer base shrink, but its Canadian and Japanese markets, both of which use metric, expand—especially after the 2011 earthquake and tsunami. Wood-product producers made adjustments so that their production systems could flex between metric and U.S. customary measures based on what their customers needed. Because so much of the world uses metric only, more and more U.S. companies are recognizing the benefits of metric as they find new international markets for their products.