June 29, 2015 report
Researchers develop algorithm to help identify patient zero in an epidemic
(Phys.org)—A team of researchers affiliated with several institutions in Croatia has developed an algorithm that is able to help pinpoint the first person who became ill when an epidemic occurred. In their paper published in the journal Physical Review Letters, the team describes how they built their algorithm, how it was tested and how accurate they believe it is.
Knowing who the first person to be infected was, when an epidemic occurs, can be very helpful to health workers trying to figure out how to combat the disease (by noting how and from which other animal it jumped from, for example) unfortunately, there are few tools available that are able to help. In this new effort, the team in Croatia used statistical tools and real data to create and test an algorithm that appears to offer a way to get closer to an original source, which they claim, can be quite accurate in some cases.
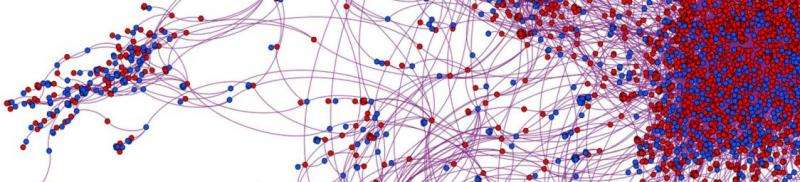
To address the problem, the researchers built a network of connected nodes to represent both infected and non-infected people in an epidemic. They then applied exact analytic calculations and Monty Carlo estimations to determine the probability of any one node on a network being patient zero. Once all the calculations have been made, the likelihood for each node is noted, if just one shows a hundred percent certainty, than the task has been completed. If there is more than one, relative certainties for each are generated.
To test their network, the researchers used real data from a web site where patrons of sex-workers could offer reviews on their experience. They found that there were able to pinpoint a single individual (or one that was just one hop away) with a 60 percent accuracy rate.
The team notes that their algorithm is more accurate when used with fast spreading diseases, and of course does better the sooner it is applied. They also note that it does not do very well when used for a small population after a period of time has passed because it can lead to every node having an equal chance of being patient zero.
The researchers also point out that their network and algorithm can be used in other areas as well, such as with assisting in finding patient zero in a computer virus epidemic, or with incidents that occur on social networks.
More information: Identification of Patient Zero in Static and Temporal Networks: Robustness and Limitations, Nino Antulov-Fantulin, Alen Lančić, Tomislav Šmuc, Hrvoje Štefančić, and Mile Šikić, Phys. Rev. Lett. 114, 248701 – Published 16 June 2015. journals.aps.org/prl/abstract/ … ysRevLett.114.248701 . On Arxiv: arxiv.org/abs/1406.2909
ABSTRACT
Detection of patient zero can give new insights to epidemiologists about the nature of first transmissions into a population. In this Letter, we study the statistical inference problem of detecting the source of epidemics from a snapshot of spreading on an arbitrary network structure. By using exact analytic calculations and Monte Carlo estimators, we demonstrate the detectability limits for the susceptible-infected-recovered model, which primarily depend on the spreading process characteristics. Finally, we demonstrate the applicability of the approach in a case of a simulated sexually transmitted infection spreading over an empirical temporal network of sexual interactions.
Journal information: Physical Review Letters , arXiv
© 2015 Phys.org