Computer simulation supports a "holographic" theory describing a black hole
A "holographic" theory, which was conjectured to describe accurately the dynamical phenomena occurring in a black hole, has been tested numerically by a research group composed of four researchers: Masanori Hanada, Ph.D., an associate professor at Kyoto University; Yoshifumi Hyakutake, Ph.D., an associate professor at Ibaraki University; Goro Ishiki, Ph.D., an assistant professor at Kyoto University; and Jun Nishimura, Ph.D., an associate professor at KEK.
Black holes are literally "black holes" residing in the cosmic space: once something goes into a black hole, it can never come out even with the speed of light. In 1974 the British physicist, Hawking, showed theoretically that a black hole actually radiates particles and evaporates little by little by considering the microscopic effect near the black hole which causes particles and anti-particles to be created and annihilated in pairs. This led him to conclude that a black hole can be viewed as an object with certain temperature. On the other hand, it has been thought difficult to understand such properties of the black hole accurately from the interior of the black hole. The reason is that as one approaches the center of the black hole, the curvature of the space-time increases, and the description of gravity in terms of general relativity breaks down.
As a new approach to solve this problem, Maldacena, a professor of Princeton University proposed a theory which describes gravity including the center of the black hole. According to this theory, dynamical phenomena occurring in a curved space-time like black holes can be described by a theory on a flat space-time, just as a hologram can record the information of 3D objects on a plane.
In the present research, Maldacena's theory has been tested by calculating the relationship between the mass and the temperature of a black hole on a computer. The results obtained for black holes of various size agreed with the results obtained by approximate calculation of quantum gravity effects based on conventional superstring theory. This goes beyond the numerous tests made so far, which have been restricted to the case in which the quantum gravity effects can be neglected. Maldacena's theory is considered to have a wider range of applicability than the approximate calculation based on conventional superstring theory. It is therefore expected that various puzzles concerning the evaporation of black holes can be solved by developing further the numerical approach established in the present work.
Background
General relativity is a theory due to Einstein, which claims that the origin of gravity is actually the curvature of the space-time. This theory has been very successful and it provided understanding of the fact that the universe is expanding and that black holes can exist in the universe. On the other hand, in order to clarify the beginning of the universe and the evaporation of black holes, it is necessary to use a microscopic description of gravity incorporating quantum gravity effects. A theory that goes beyond general relativity in this respect has therefore been pursued.
Pioneering papers which discussed the use of "hologram" in gravity theory including black holes are the ones by 't Hooft (1993) and Susskind (1995). What Maldacena did was to propose an explicit physical system corresponding to the "hologram" based on studies of superstring theory, which is the most promising candidate of a microscopic description of gravity incorporating quantum gravity effects. Maldacena's theory has been verified from various angles by many researchers in the past fifteen years or so. But the previous analytic studies were mostly restricted to the situation in which the quantum gravity effects near the black hole can be neglected, and there was very little clue as to the correctness of the theory beyond this restriction. Numerical methods using computers have been expected to enable concrete calculations on Maldacena's theory beyond this restriction and to make a breakthrough by providing a test including the quantum gravity effects.
Content of the Research and Its Achievement
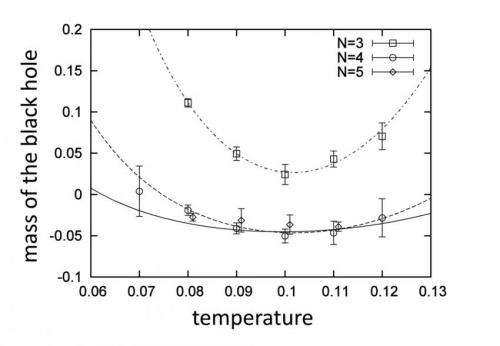
According to Maldacena, one can study various properties of a black hole such as the relationship between the mass and the temperature by using the theory corresponding to the "hologram" of the black hole. In the present research, the mass of a black hole was computed on a computer based on Maldacena's theory, and the results were compared with the results obtained by approximate calculation based on conventional superstring theory, which incorporate the quantum gravity effects (Fig. 1).
Denoting the number of elements composing the black hole by N, previous works mainly studied the case in which N is so large that the quantum gravity effects near the black hole can be neglected. In the case of small N, on the other hand, whether the theory really describes the black hole correctly was an open question.
In Fig. 1 the results obtained for N = 3, 4, 5 are shown, where N is the number of elements composing the black hole. As N decreases, the corresponding black hole becomes smaller and hence the curvature at the surface of the black hole becomes larger. Thus the quantum gravity effects become more prominent. It was known that the same effects make the black hole unstable, and cause technical difficulty in the computation. In the present research, this difficulty has been overcome by developing a new calculation method, which enabled the researchers to obtain the results for the mass of the black hole.
Based on the observation that the two different theoretical results agree, it has been concluded that the results obtained by the calculation in Maldacena's theory include the quantum gravity effects correctly as the calculation in conventional superstring theory does. (Note, however, that the calculation in conventional superstring theory is merely an approach from the exterior of the black hole, which enables estimation of the quantum gravity effects near the black hole as far as they are not too strong. On the other hand, Maldacena's theory describes the interior of the black hole and it is expected to be valid even in the case in which the quantum gravity effects near the black hole are strong.)
This work was published in the online version of the Science Express (April 17, 2014).
The Significance of This Work and Future Prospects
This work tested Maldacena's theory concerning a new description of black holes using a "hologram." While previous works provided various tests under the situation in which the quantum gravity effects near the black hole can be neglected, this work made a step forward and succeeded in performing a test including the quantum gravity effects, which is considered a significant progress. The obtained results strongly suggest that Maldacena's theory describes the interior of the black hole even in the case in which the quantum gravity effects near the black hole cannot be neglected. It is expected that various puzzles concerning the evaporation of black holes can be clarified by extending the present work further.
For instance, within the approximation used by Hawking, it was concluded that one cannot extract the information of the objects which fell into the black hole from the radiation emitted from the black hole. This is called the "information loss problem" associated with the evaporation of black holes, and it has been considered a serious paradox between general relativity and quantum mechanics, which constitute the two bases of contemporary physics established in the twentieth century.
It should be emphasized that the present work is a sort of continuation of previous works, and the results are obtained in the stream of various research activities on the subject. Also, Maldacena's theory, which is a concrete realization of the physical system that represents the "hologram," can be regarded as a new approach to superstring theory, which is the most promising candidate of quantum theory of gravity. It is therefore expected that the present work triggers further development of Maldacena's theory or superstring theory, which would enable physicists to clarify the beginning of the universe and the composition of the universe, in which quantum gravity effects are thought to be important.
More information: "Holographic Description of a Quantum Black Hole on a Computer" M. Hanada, Y. Hyakutake, G. Ishiki and J. Nishimura, DOI: 10.1126/science.1250122
Journal information: Science Express