Short algorithm, long-range consequences
In the last decade, theoretical computer science has seen remarkable progress on the problem of solving graph Laplacians—the esoteric name for a calculation with hordes of familiar applications in scheduling, image processing, online product recommendation, network analysis, and scientific computing, to name just a few. Only in 2004 did researchers first propose an algorithm that solved graph Laplacians in "nearly linear time," meaning that the algorithm's running time didn't increase exponentially with the size of the problem.
At this year's ACM Symposium on the Theory of Computing, MIT researchers will present a new algorithm for solving graph Laplacians that is not only faster than its predecessors, but also drastically simpler. "The 2004 paper required fundamental innovations in multiple branches of mathematics and computer science, but it ended up being split into three papers that I think were 130 pages in aggregate," says Jonathan Kelner, an associate professor of applied mathematics at MIT who led the new research. "We were able to replace it with something that would fit on a blackboard."
The MIT researchers—Kelner; Lorenzo Orecchia, an instructor in applied mathematics; and Kelner's students Aaron Sidford and Zeyuan Zhu—believe that the simplicity of their algorithm should make it both faster and easier to implement in software than its predecessors. But just as important is the simplicity of their conceptual analysis, which, they argue, should make their result much easier to generalize to other contexts.
Overcoming resistance
A graph Laplacian is a matrix—a big grid of numbers—that describes a graph, a mathematical abstraction common in computer science. A graph is any collection of nodes, usually depicted as circles, and edges, depicted as lines that connect the nodes. In a logistics problem, the nodes might represent tasks to be performed, while in an online recommendation engine, they might represent titles of movies.
In many graphs, the edges are "weighted," meaning that they have different numbers associated with them. Those numbers could represent the cost—in time, money or energy—of moving from one step to another in a complex logistical operation, or they could represent the strength of the correlations between the movie preferences of customers of an online video service.
The Laplacian of a graph describes the weights between all the edges, but it can also be interpreted as a series of linear equations. Solving those equations is crucial to many techniques for analyzing graphs.
One intuitive way to think about graph Laplacians is to imagine the graph as a big electrical circuit and the edges as resistors. The weights of the edges describe the resistance of the resistors; solving the Laplacian tells you how much current would flow between any two points in the graph.
Earlier approaches to solving graph Laplacians considered a series of ever-simpler approximations of the graph of interest. Solving the simplest provided a good approximation of the next simplest, which provided a good approximation of the next simplest, and so on. But the rules for constructing the sequence of graphs could get very complex, and proving that the solution of the simplest was a good approximation of the most complex required considerable mathematical ingenuity.
Looping back
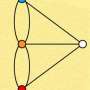
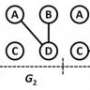
The MIT researchers' approach is much more straightforward. The first thing they do is find a "spanning tree" for the graph. A tree is a particular kind of graph that has no closed loops. A family tree is a familiar example; there, a loop might mean that someone was both parent and sibling to the same person. A spanning tree of a graph is a tree that touches all of the graph's nodes but dispenses with the edges that create loops. Efficient algorithms for constructing spanning trees are well established.
The spanning tree in hand, the MIT algorithm then adds back just one of the missing edges, creating a loop. A loop means that two nodes are connected by two different paths; on the circuit analogy, the voltage would have to be the same across both paths. So the algorithm sticks in values for current flow that balance the loop. Then it adds back another missing edge and rebalances.
In even a simple graph, values that balance one loop could imbalance another one. But the MIT researchers showed that, remarkably, this simple, repetitive process of adding edges and rebalancing will converge on the solution of the graph Laplacian. Nor did the demonstration of that convergence require sophisticated mathematics: "Once you find the right way of thinking about the problem, everything just falls into place," Kelner explains.
Provided by Massachusetts Institute of Technology