Explained: Graphs
When most people hear the word "graph," an image springs to mind: a pair of perpendicular lines overlaid with a line, a curve, or bars of different heights.
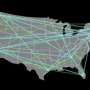
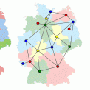
But when computer scientists use the term, they often have something very different in mind. The most familiar example of a graph, in the computer-science sense, may be a network diagram, with computers or routers depicted as circles and the connections between them depicted as line segments. But graphs can represent all kinds of things, from sequences of decisions to relationships between data in a database, and they play a crucial role in a huge number of algorithms.
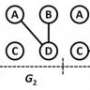
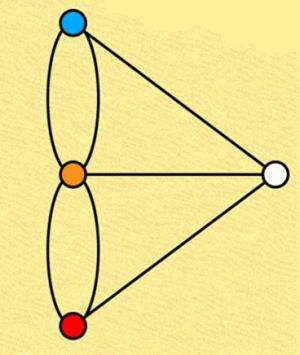
Technically, a graph consists of two fundamental elements: nodes (or vertices, usually depicted as circles) and edges (usually depicted as lines connecting nodes). Often, in computer science, the edges are "weighted": Associated with each edge is a number that indicates the ease or difficulty of traversing it. The weight of an edge could, for instance, represent the bandwidth of a wired connection in a network, or it could represent the cost—in money, computational resources or something else—in moving from one step to the next in some process.
Mathematicians have developed a handful of standard techniques for describing graphs: The weights of edges, for instance, can be depicted in a big table that maps every node against every other. In computer science, the challenge posed by graphs generally lies in their analysis, not their representation. Sometimes that analysis requires careful consideration of the data represented by each node. Other times, the point of graphic analysis is precisely to abstract away from the data: The useful information is some general property of the network as a whole.
A glance at some recent MIT News articles provides, to coin a phrase, graphic evidence of the importance of graphs. Last month, MIT professor of mathematics Peter Shor, his former student Ramis Movassagh and their colleagues published a paper demonstrating properties of physical systems that could make them useful for quantum computing. Their proof relied, in part, on graphs whose nodes represented the quantum states of physical systems; edges connected states that could be reached from each other with no change in energy. There, the crucial revelation was that the graph was highly connected: There were no bottlenecks that transitions between states had to traverse.
An August paper by Alvin Cheung, a graduate student in the Department of Electrical Engineering and Computer Science; his advisor, professor of computer science and engineering Sam Madden; and colleagues at Cornell University describes an algorithm that uses graphs to represent discrete instructions in computer programs. Like Shor and Movassagh, Cheung and Madden were looking at edges, not nodes. But unlike Shor and Movassagh, they were using a weighted graph, where the edges depicted the amount of data that each new instruction inherited from the last. Cheung and Madden's algorithm automatically splits a computer program up so that it can run on multiple servers; by identifying edges with low weights, it minimizes the data that has to pass between servers, improving efficiency.
Finally, in another paper that appeared last month, Daniela Rus, a professor of computer science and engineering and director of MIT's Computer Science and Artificial Intelligence Laboratory, her postdoc Dan Feldman, and Cynthia Sung, a graduate student in her group, described an algorithm that uses a particular type of graph called a tree. There, the interest was all in the nodes, not the edges. The most familiar example of a tree may be a family-tree diagram, which has a single node at the top and fans out at successive layers of depth. In the Rus group's algorithm, the bottom layer of the tree represented raw GPS data, and all the other nodes represented compressed versions of the data contained in the nodes beneath them.
That's just a few recent examples. Many algorithms model decision problems as graphs: For instance, a chess-playing algorithm might treat a game of chess as a tree in which each node represents a state of the board, and the nodes beneath it represent possible moves. Others use weighted graphs to depict the strength of the correlations between data points in a database. Some major advances in computer science involve problems that are specified using graphs in the first place, such as the "max-flow" problem, which is at the heart of a huge range of logistical analyses. And that's to say nothing of perhaps the most intuitive use of graphs, in the analysis of communication networks.
More information: OpenCourseWare: "Introduction to Graph Theory"—ocw.mit.edu/courses/mathematic … pring-2005/index.htm
Provided by Massachusetts Institute of Technology
This story is republished courtesy of MIT News (web.mit.edu/newsoffice/), a popular site that covers news about MIT research, innovation and teaching.