More-efficient computation: Finding local solutions to overwhelmingly complex problems

At a time when the Internet puts an untold amount of information at anyone’s fingertips, and automated scientific experiments churn out data faster than researchers can keep up with it, and communications networks can include billions of people, even the simplest computational tasks can become so enormous that they would overwhelm even a powerful supercomputer. But sometimes it’s enough to know just a little bit about the solution to a monstrous calculation: biologists mining genomic data, for instance, might be interested in just a handful of genes.

At the Innovations in Computer Science conference at Tsinghua University earlier this year, MIT researchers, together with colleagues at Tel Aviv University, presented a new mathematical framework for finding such localized solutions to complex calculations. They applied their approach to some classic problems in computer science, which involve mathematical abstractions known as graphs.

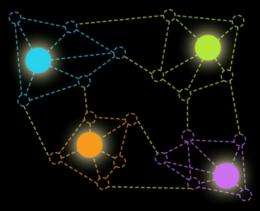
The most familiar example of a graph is probably a diagram of a communications network, where the nodes of the network — the communications devices — are depicted as circles, and the connections between them are depicted as lines. A graph is any such combination of circles and lines, or, as mathematicians say, of vertices and edges. A flow chart is another example of a graph; or a graph could depict citations of scientific papers, where every vertex is a paper, connected by edges to the papers that cite it.

Graphs can represent an endless diversity of data, but for any given graph, it’s often useful to compute what’s called a maximal independent set. An independent set is one where enough vertices have been deleted from the graph that there are no longer any edges: the remaining vertices are desert islands, none connected to any other. An independent set is maximal if trying to restore any of the deleted vertices will also restore an edge. That is, every vertex left out of the set is connected to one of the vertices in the set.

Community representatives

Each vertex in a maximal independent set thus stands in for a cluster of connected vertices. If the graph represents a mesh of citations, for instance, a cluster could be a set of papers on related topics.

A graph could have many different maximal independent sets, and for a large enough graph, computing even one of them could be a prohibitively time-consuming chore. Ning Xie, a graduate student in the Department of Electrical Engineering and Computer Science; his advisor, computer science professor Ronitt Rubinfeld; and Shai Vardi and Gil Tamir of Tel Aviv University devised a method to efficiently determine, for a particular region of a graph, which vertices are and are not included in at least one of the graph’s maximal independent sets. The key to the researchers’ system is that, without having to specify the entire set, they can guarantee that applying their algorithm to a second region of the graph — or a dozen or a hundred other regions — will yield results consistent with the first.

The researchers’ paper is theoretical: the researchers don’t apply their algorithm to any particular problems. But problems in research areas as diverse as bioinformatics, chemistry, artificial intelligence, scheduling and networking have been characterized as problems of calculating independent sets.

Seshadhri Comandur, a computer science researcher at Sandia National Labs in Livermore, Calif., points out that — as the researchers acknowledge in their paper — others have previously proposed particular algorithms for calculating local solutions of complex problems. “There have been lots of related concepts that have been sort of floating around,” he says, but the MIT and Tel Aviv researchers “have formalized it in an interesting way and, I think, the correct way.” He adds that he’s intrigued to see whether other local-computation algorithms can also be subsumed under the researchers’ new framework. “There are a lot of other results that have a similar flavor,” he says.

---

This story is republished courtesy of MIT News (web.mit.edu/newsoffice/), a popular site that covers news about MIT research, innovation and teaching.