New breakthrough in bubble research

A researcher from the University of Bath has found a new approach to an old geometric problem of modelling the most efficient way of packing shapes to form a foam.
The discovery is not only making waves in the mathematical world, but could also lead to medical advances in creating hip replacements and replacement bone tissue for bone cancer patients.
The 'Kelvin problem', posed by Lord Kelvin in 1887, was to find the most efficient way of splitting space into cells of equal volume with the least area of surface between them.
Kelvin's solution to the problem was a honeycomb of truncated octahedrons - shapes with six square faces and eight hexagonal faces.
A better solution was devised by physicists Weaire and Phelan at Trinity College Dublin who created a honeycomb structure which inspired the striking architecture of the Water Cube aquatic centre that featured in the 2008 Beijing Olympics.
The Weaire-Phelan structure is composed of two different shapes: an irregular pentagonal dodecahedron (12-faced polyhedron) and a polyhedron with 14 faces.
Whilst studying the honeycomb-like structure of bone replacement materials for his PhD in Mechanical Engineering at the University of Bath, Ruggero Gabbrielli devised a different way of mathematically modelling foams. His structure is instead composed of four different shapes that fit together.
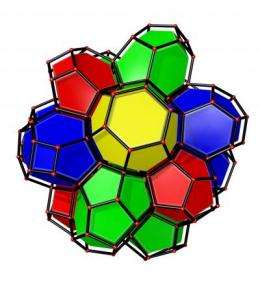
Whilst this new shape doesn't beat the Weaire-Phelan structure in terms of packing efficiency, the methods he used are a new way of approaching the problem and could ultimately lead to a better solution to the Kelvin problem.
Ruggero, who has now completed his PhD and is continuing his research at Swansea University, explained: "I'm hoping that the method will lead to an even better solution of the Kelvin problem or to a proof of the Weaire-Phelan structure optimality.
"The method uses a partial differential equation, well-known in two-dimensional pattern formation. The novelty is that I've applied it to a three-dimensional problem to model the shape of foams."
The structures he has made are also much closer to the structures of the foams found in nature.
His structure and methods, published in Philosophical Magazine Letters, have already grabbed the attention of mathematicians, chemists and physicists across the world.
Ruggero was recently invited to the USA and to Australia to talk about his new structure and discuss his methods with top mathematicians.
He said: "The journey to Pennsylvania was fantastic. In two weeks I met with two of the greatest mathematicians in the US - Thomas Hales and Ken Brakke - and the physicist Randall Kamien at the University of Pennsylvania."
Physicists Barry Ninham and Stephen Hyde then invited him to Canberra, where the structure was shown to a broader audience.
Ruggero said: "It's not just about bubbles. Three-dimensional patterns spontaneously arise in many systems nature designed."
More information: Gabbrielli, R. “A new counter-example to Kelvin’s conjecture on minimal surfaces” is published in Philosophical Magazine Letters 89 (8): 483-491.
Source: University of Bath (news : web)


















