Mathematicians set world record in packing puzzle
(PhysOrg.com) -- Finding the best way to pack the greatest quantity of a specifically shaped object into a confined space may sound simple, yet it consistently has led to deep mathematical concepts and practical applications, such as improved computer security codes.
When mathematicians solved a famed sphere-packing problem in 2005, one that first had been posed by renowned mathematician and astronomer Johannes Kepler in 1611, it made worldwide headlines.
Now, two Princeton University researchers have made a major advance in addressing a twist in the packing problem, jamming more tetrahedra -- solid figures with four triangular faces -- and other polyhedral solid objects than ever before into a space. The work could result in better ways to store data on compact discs as well as a better understanding of matter itself.
In the cover story of the Aug. 13 issue of Nature, Salvatore Torquato, a professor in the Department of Chemistry and the Princeton Institute for the Science and Technology of Materials, and Yang Jiao, a graduate student in the Department of Mechanical and Aerospace Engineering, report that they have bested the world record, set last year by Elizabeth Chen, a graduate student at the University of Michigan.
Using computer simulations, Torquato and Jiao were able to fill a volume to 78.2 percent of capacity with tetrahedra. Chen, before them, had filled 77.8 percent of the space. The previous world record was set in 2006 by Torquato and John Conway, a Princeton professor of mathematics. They succeeded in filling the space to 72 percent of capacity.
Beyond making a new world record, Torquato and Jiao have devised an approach that involves placing pairs of tetrahedra face-to-face, forming a "kissing" pattern that, viewed from the outside of the container, looks strangely jumbled and irregular.
"We wanted to know this: What's the densest way to pack space?" said Torquato, who is also a senior faculty fellow at the Princeton Center for Theoretical Science. "It's a notoriously difficult problem to solve, and it involves complex objects that, at the time, we simply did not know how to handle."
Henry Cohn, a mathematician with Microsoft Research New England in Cambridge, Mass., said, "What's exciting about Torquato and Jiao's paper is that they give compelling evidence for what happens in more complicated cases than just spheres." The Princeton researchers, he said, employ solid figures as a "wonderful test case for understanding the effects of corners and edges on the packing problem."
Studying shapes and how they fit together is not just an academic exercise. The world is filled with such solids, whether they are spherical oranges or polyhedral grains of sand, and it often matters how they are organized. Real-life specks of matter resembling these solids arise at ultra-low temperatures when materials, especially complex molecular compounds, pass through various chemical phases. How atoms clump can determine their most fundamental properties.
"From a scientific perspective, to know about the packing problem is to know something about the low-temperature phases of matter itself," said Torquato, whose interests are interdisciplinary, spanning physics, applied and computational mathematics, chemistry, chemical engineering, materials science, and mechanical and aerospace engineering.
And the whole topic of the efficient packing of solids is a key part of the mathematics that lies behind the error-detecting and error-correcting codes that are widely used to store information on compact discs and to compress information for efficient transmission around the world.
Beyond solving the practical aspects of the packing problem, the work contributes insight to a field that has fascinated mathematicians and thinkers for thousands of years. The Greek philosopher Plato theorized that the classical elements -- earth, wind, fire and water -- were constructed from polyhedra. Models of them have been found among carved stone balls created by the late Neolithic people of Scotland.
The tetrahedron, which is part of the family of geometric objects known as the Platonic solids, must be packed in the face-to-face fashion for maximum effect. But, for significant mathematical reasons, all other members of the Platonic solids, the researchers found, must be packed as lattices to cram in the largest quantity, much the way a grocer stacks oranges in staggered rows, with successive layers nestled in the dimples formed by lower levels. Lattices have great regularity because they are composed of single units that repeat themselves in exactly the same way.
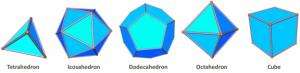
Mathematicians define the five shapes composing the Platonic solids as being convex polyhedra that are regular. For non-mathematicians, this simply means that these solids have many flat faces, which are plane figures, such as triangles, squares or pentagons. Being regular figures, all angles and faces' sides are equal. The group includes the tetrahedron (with four faces), the cube (six faces), the octahedron (eight faces), the dodecahedron (12 faces) and the icosahedron (20 faces).
There's a good reason why tetrahedra must be packed differently from other Platonic solids, according to the authors. Tetrahedra lack a quality known as central symmetry. To possess this quality, an object must have a center that will bisect any line drawn to connect any two points on separate planes on its surface. The researchers also found this trait absent in 12 out of 13 of an even more complex family of shapes known as the Archimedean solids.
The conclusions of the Princeton scientists are not at all obvious, and it took the development of a complex computer program and theoretical analysis to achieve their groundbreaking results. Previous computer simulations had taken virtual piles of polyhedra and stuffed them in a virtual box and allowed them to "grow."
The algorithm designed by Torquato and Jiao, called "an adaptive shrinking cell optimization technique," did it the other way. It placed virtual polyhedra of a fixed size in a "box" and caused the box to shrink and change shape.
There are tremendous advantages to controlling the size of the box instead of blowing up polyhedra, Torquato said. "When you 'grow' the particles, it's easy for them to get stuck, so you have to wiggle them around to improve the density," he said. "Such programs get bogged down easily; there are all kinds of subtleties. It's much easier and productive, we found, thinking about it in the opposite way."
Cohn, of Microsoft, called the results remarkable. It took four centuries, he noted, for mathematician Tom Hales to prove Kepler's conjecture that the best way to pack spheres is to stack them like cannonballs in a war memorial. Now, the Princeton researchers, he said, have thrown out a new challenge to the math world. "Their results could be considered a 21st Century analogue of Kepler's conjecture about spheres," Cohn said. "And, as with that conjecture, I'm sure their work will inspire many future advances."
Many researchers have pointed to various assemblies of densely packed objects and described them as optimal. The difference with this work, Torquato said, is that the algorithm and analysis developed by the Princeton team most probably shows, in the case of the centrally symmetric Platonic and Archimedean solids, "the best packings, period."
Their simulation results are also supported by theoretical arguments that the densest packings of these objects are likely to be their best lattice arrangements. "This is now a strong conjecture that people can try to prove," Torquato said.
Source: Princeton University
















