Scientists confirm existence of quantum knots and create them in a quantum-mechanical field

The very first experimental observations of knots in quantum matter have just been reported in Nature Physics.
Scientists at Aalto University (Finland) and Amherst College (USA) have created knotted solitary waves, or knot solitons, in the quantum-mechanical field describing a gas of superfluid atoms, also known as a Bose–Einstein condensate.
In contrast to knotted ropes, these quantum knots exist in a field that assumes a certain direction at every point of space. The field segregates into an infinite number of linked rings, each with its own field direction. The resulting structure is topologically stable as it cannot be separated without breaking the rings. In other words, one cannot untie the knot within the superfluid unless one destroys the state of the quantum matter.
"To make this discovery, we exposed a Rubidium condensate to rapid changes of a specifically tailored magnetic field, tying the knot in less than a thousandth of a second. After we learned how to tie the first quantum knot, we have become rather good at it. Thus far, we have tied several hundred such knots," says Professor David Hall, Amherst College.
The scientists tied the knot by squeezing the structure into the condensate from its outskirts. This required them to initialize the quantum field to point in a particular direction, after which they suddenly changed the applied magnetic field to bring an isolated null point, at which the magnetic field vanishes into the center of the cloud. Then they just waited for less than a millisecond for the magnetic field to do its trick and tie the knot.
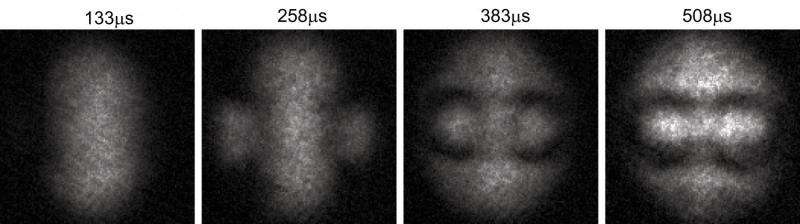
"For decades, physicists have been theoretically predicting that it should be possible to have knots in quantum fields, but nobody else has been able to make one. Now that we have seen these exotic beasts, we are really excited to study their peculiar properties. Importantly, our discovery connects to a diverse set of research fields including cosmology, fusion power, and quantum computers," says research group leader Mikko Möttönen, Aalto University.
Knots have been used and appreciated by human civilizations for thousands of years. For example, they have enabled great seafaring expeditions and inspired intricate designs and patterns. The ancient Inca civilization used a system of knots known as quipu to store information. In modern times, knots have been thought to play important roles in the quantum-mechanical foundations of nature, although they have thus far remained unseen in quantum dynamics.
In everyday life, knots are typically tied on ropes or strings with two ends. However, these kinds of knots are not what mathematicians call topologically stable since they can be untied without cutting the rope. In stable knots, the ends of the ropes are glued together. Such knots can be relocated within the rope but cannot be untied without scissors.

Mathematically speaking, the created quantum knot realizes a mapping referred to as Hopf fibration that was discovered by Heinz Hopf in 1931. The Hopf fibration is still widely studied in physics and mathematics. Now it has been experimentally demonstrated for the first time in a quantum field.
"This is the beginning of the story of quantum knots. It would be great to see even more sophisticated quantum knots to appear such as those with knotted cores. Also it would be important to create these knots in conditions where the state of the quantum matter would be inherently stable. Such system would allow for detailed studies of the stability of the knot itself," says Mikko Möttönen.
More information: D. S. Hall et al. Tying quantum knots, Nature Physics (2016). DOI: 10.1038/NPHYS3624
Journal information: Nature Physics
Provided by Aalto University