Strings attached to future high temperature superconductivity
The behaviour of strongly correlated electron systems, such as high temperature superconductors, defies explanation in the language of ordinary quantum theory. A seemingly unrelated area of physics, string theory, might give physicists a better understanding of the weird behaviour of this kind of collective electron system. A bird's eye view was recently published in Nature by five world experts in the field, among which Jan Zaanen from Leiden University/Delta Institute for Theoretical Physics.
Higher and higher
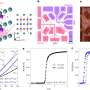
Up until the mid-1980s, it was commonly thought that superconductivity – the complete loss of electrical resistance in a material – only occurred at temperatures below 30 K. The discovery of high-temperature superconductivity in copper oxides (1986) ranks among the major scientific events of the 20th century. In less than a decade, temperatures went up to a mind-blowing 165 K, promising room temperature superconductivity in a near future. But to reach that point, new theoretical descriptions are indispensable. That is the take-home message from an extensive review in this week's Nature by five leading experts in the field.
Electrons joining hands
Conventional superconductors can be described by an extremely successful theory, developed in the late 1950's by John Bardeen, Leon Cooper and John Schrieffer (Nobel Prize 1972). Their theory describes how, at low enough temperatures, single electrons in a metal join hands and form so-called Cooper pairs. According to ordinary quantum theory, these paired electrons behave as one single particle with new properties. The most important: such a Cooper pair can travel freely, without any resistance at all, through the material.
Strange behaviour
That description fails completely in high-temperature superconductors. For example, at temperatures well above the superconductivity threshold, the copper oxides behave very peculiarly. Above this threshold, the copper oxides were expected to behave like normal metals, with a certain amount of conductivity. Instead, the conductivity in modern superconducting materials is much, much smaller than in simple metals, hence their nickname 'strange – or bad – metals'.
In search of a new theory
With a bird's eye view, Jan Zaanen and his co-authors describe the recent developments in the field of high-temperature superconductors and connect them to strongly correlated electron systems in general. Zaanen says: "These are all collective systems with huge numbers of electrons, and ordinary quantum theory just doesn't suffice to describe them. We are desperately in need of a new theory.' That theory, the authors elaborate, could very well be one that originates in a completely unrelated field of physics: string theory.
Holographic duality
In string theory, there exist many dualities: equivalent descriptions of a problem in two different ways. Depending on the problem, one description is usually easier than the other. The most famous duality was discovered by Juan Maldacena in 1997. This so-called AdS/CFT duality connects quantum field theory with a theory of gravity. It turns out that there is a holographic connection between the two, for which the field theory can be thought of as living on the boundary of an anti-deSitter space.
Mathematical toolbox
In 2007, theoretical physicists like Jan Zaanen started to use this holographic duality as a mathematical toolbox to play around with in the field of superconductors. To their surprise, it turned out that certain weird aspects, such as the behaviour of 'strange metals', can be described as the holographic dual of a black hole. That doesn't mean there are real black holes in superconductors, but the same mathematical tools can be used to describe both phenomena.
As a bonus, string theory also benefits from this exchange of tools, especially in the field of quantum information. With hot topics such as large scale entanglement, there are many similarities with strongly correlated electron systems such as superconductors.
A revolution in physics?
The authors conclude their extensive review with the remark that 'The jury is still out on whether this is a coincidence or signals the onset of a revolution in physics.' But when asked, Jan Zaanen is more outspoken: "I think we are facing a revolution."
More information: "From quantum matter to high-temperature superconductivity in copper oxides," B.Keimer, S.A. Kivelson, M.R. Norman, S. Uchida & J. Zaanen, in: Nature 12 Feb 2015. DOI: 10.1038/nature14165
Journal information: Nature
Provided by Leiden University