May 28, 2014 feature
A matter of matter: Demonstrating destructive quantum interference using Bose-Einstein condensates
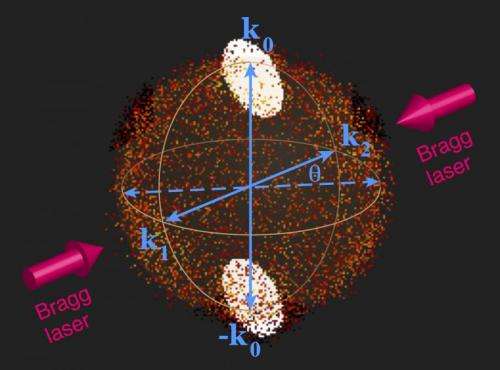
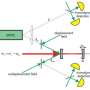
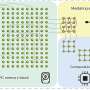
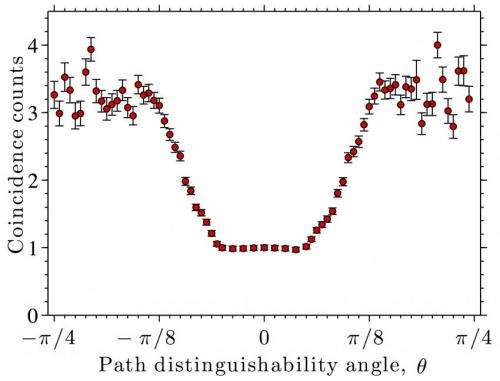
(Phys.org) —When C. K. Hong, Z. Y. Ou and Leonard Mandel demonstrated destructive quantum interference between pairs of indistinguishable bosons in their 1987 paper1, they did so with massless photons. Their protocol – christened the Hong–Ou–Mandel (HOM) effect – remained unchanged until recently, when scientists at The University of Queensland, Brisbane proposed an experiment to implement HOM in the matter-wave regime. This massive-particle version of the HOM effect uses pair-correlated atoms produced in a collision of two Bose–Einstein condensates and subjected to two laser-induced so-called Bragg pulses. (A Bose-Einstein condensate, or BEC, is a phase of matter in which bosons in a dilute gas enter the same quantum state when cooled to a temperature near absolute zero – that is, 0 K or −273.15 °C – and macroscopic-scale quantum effects appear. Bragg pulses replicate atom optics analogs of the mirror and beam-splitter elements of the photonic HOM interferometer.) By simulating the atom-optics HOM effect using colliding condensates and predicting an interference visibility of about 70%, the researchers say that their matter-wave approach may lead to stronger tests of quantum mechanics, including Bell inequality violations and the Einstein–Podolsky–Rosen paradox, the latter now being known as entanglement.
Doctoral student Robert Lewis-Swan and Prof. Karen Kheruntsyan discussed the paper they published in Nature Communications. In designing an experiment to investigate the HOM effect in a matter-wave context and formulating the measurement protocol for a multimode matter-wave field, the researchers encountered a number of challenges. "An obvious technical challenge in putting together this experimental proposal was the ability to numerically simulate the entire experiment using the computational resources available to us," Lewis-Swan tells Phys.org. "These real-time quantum dynamical simulations – when performed in experimentally realistic parameter regimes – are extremely challenging and require the use of supercomputing cluster facilities for parallel computing. We've been fortunate to have access to such a supercomputing cluster facility locally at the University of Queensland."
Another major conceptual challenge, Kheruntsyan adds, was the need to keep their proposal experimentally realizable using the existing technologies in the field of ultra-cold atoms. "For example, we had to be conscious about the challenges in getting statistically significant data using the existing atom detectors that have relatively low detection efficiency. Acquiring such data requires repeated runs of the experiment, typically in many thousands, which in turn requires a continuous, stable operation of the experimental apparatus for several weeks." It is indeed critical to maintain stable operation of the Bose-Einstein condensate apparatus over such extended periods of time – a very challenging task for the experimentalists. "Moreover, prior to coming up with the measurement protocol presented in the paper, we had an alternative protocol, which – while being in a more direct analogy with the optical HOM experiment – had the disadvantage of requiring a significantly larger number of experimental runs. It therefore took as a while to explore other alternatives until we came up with the current idea."
In their paper, Lewis-Swan and Kheruntsyan write that a matter-wave demonstration of the HOM effect would enable an expansion of foundational tests of quantum mechanics into previously unexplored regimes, and discuss the possibility of implementing an experiment based on their simulation that could demonstrate a Bell inequality violation using an atom-optics adaptation of the Rarity–Tapster setup2. Bell's inequality (also referred to as Bell's theorem) is a so-called no-go theorem – that is, one that states that a particular situation is not physically possible if one adopts a local realistic interpretation of quantum theory (a combination of the principle of locality with the "realistic" assumption that all physical quantities must objectively have a pre-existing value for any possible measurement before the measurement is actually made) – articulating an important distinction between so called local hidden variable theories and quantum mechanics. Bell posited3 that any physical theory incorporating local realism cannot reproduce all predictions made by quantum mechanics, doing so in response to a paper by Albert Einstein and co-authors Boris Podolsky and Nathan Rosen4 asserting (in what has come to be referred to as the EPR paradox) that quantum mechanics is incomplete and that it must be supplemented by local hidden variables if one wants to understand nonlocal entanglement (which Einstein famously referred to as "spooky action at a distance") while preserving a local realistic interpretation of quantum theory.
"It's important to understand that the EPR/Bell argument is not about classical versus quantum mechanics," Kheruntsyan emphasizes, "but rather about the interpretation of quantum mechanical observables and quantum nonlocality, which permits nonlocal entanglement on the one hand, and the EPR-presumption that any physical theory must have a local realistic interpretation, in which case nonlocal entanglement renders quantum mechanics as an incomplete theory and necessitates the introduction of local hidden variables and hidden variable theories as alternatives to quantum mechanics."
Kheruntsyan tells Phys.org that demonstrating the HOM effect with matter waves would imply the existence of strong quantum correlations between the atoms derived from colliding condensates. "Such correlations are a necessary but not sufficient condition for demonstrating a Bell inequality violation." He points out that Bell inequality violations have been so far demonstrated in numerous experiments with massless photons, but only rarely with massive particles. "Therefore," he adds, "there's still a lot to be learned and understood about Bell inequality violations with massive particles, such as scaling with particle mass and relative distance – or indeed the total number of particles involved in the violation, which in turn would mean extending the regimes of applicability of the concept of quantum nonlocality to mesoscopic and perhaps even macroscopic realms." As it turns out, researchers at the University of Oxford may have shown just that by entangling millimeter-sized diamonds at room temperature5.
Kheruntsyan says that in addition to condensate collisions, their protocol could be easily applied to condensate dissociation of diatomic molecules. That said, he acknowledges one of the major limitations in using them as an alternative source of pair-correlated atoms, which is that such condensates currently have very short lifetimes. At the same time, he adds, other techniques not requiring Bose-Einstein condensates are possible – an example being a controlled preparation and manipulation of exactly two identical atoms trapped by optical tweezers, which is a technique currently being pursued at the University of Colorado, Boulder. (Optical tweezers, or single-beam gradient force traps, use a highly-focused laser beam to provide an attractive or repulsive force to physically hold and move microscale objects.) "The optical tweezer setup, however, does not appear suitable for implementing the Rarity-Tapster scheme for a Bell inequality test – which is what we see as the next major step in extending our experimental proposal. The idea here is to tune the Bragg pulses to realize two separate HOM-interferometer arms, enabling us to mix two angle-resolved pairs of momentum modes from the collisional halo. This, in turn, would then form the basis for the prototype Bell state." The Rarity-Tapster scheme measures correlations that violate a form of Bell's inequality in the properties of massive entangled particles6.
Interestingly, the HOM interferometer produces a highly entangled output state that is well-suited for studying entanglement in general – and the problem of decoherence, or entanglement sudden death (ESD), in particular. However, further research is required to determine whether their scheme may allow ESD to be delayed or prevented by mitigating decoherence, as has been shown by using weak measurement and quantum measurement reversal7.
There are also other areas of research that might benefit from the study. "The HOM effect is a classic example of fundamental research – demonstrating quantum mechanical interference between indistinguishable atoms, without necessarily an immediate technological benefit," Kheruntsyan points out. "Having said this, it's worth remembering that in the original photonic experiment, the HOM-interference scheme was actually used for a practical purpose—namely, as a means of overcoming the limited 100 picosecond resolution time of a single photodetector to achieve unprecedented resolution in detecting subpicosecond time intervals between pairs of photons and, by implication, the length of a subpicosecond photon wave packet." The researchers' proposed matter-wave version of the HOM experiment could in principle be used for precision measurement of, for example, the spatial coherence length of a single-mode atomic wave packet. However, he says, their current multimode setup is not amenable to direct implementation of this idea.
"So, as of now," Kheruntsyan concludes, "we envisage that the next major development of our research lies in extending the proposed scheme to a Bell inequality test. The ultimate goal here would be to generate and demonstrate quantum mechanical entanglement between pairs of space-like separated atoms."
More information: Proposal for demonstrating the Hong–Ou–Mandel effect with matter waves, Nature Communications 5:3752 (2014), doi:10.1038/ncomms4752
Related:
1Measurement of subpicosecond time intervals between two photons by interference, Physical Review Letters 59, 2044 (2 November 1987), doi:10.1103/PhysRevLett.59.2044
2Experimental violation of Bell's inequality based on phase and momentum, Physical Review Letters 64:2495 (21 May 1990), doi:10.1103/PhysRevLett.64.2495
3On the Einstein-Podolsky-Rosen paradox, Physics Vol. 1 (1964), pp. 195-200 (PDF)
4Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Physical Review 47:777 (15 May 1935), doi:10.1103/PhysRev.47.777 (PDF)
5Entangling Macroscopic Diamonds at Room Temperature, Science 2 December 2011:Vol. 334 no. 6060 pp. 1253-1256, doi:10.1126/science.1211914
6Experimental violation of a Bell's inequality with efficient detection, Nature 409, 791-794 (15 February 2001), doi:10.1038/35057215
7Protecting entanglement from decoherence using weak measurement and quantum measurement reversal, Nature Physics 8, 117–120 (2012), doi:10.1038/nphys2178
Journal information: Nature Communications , Physical Review Letters , Science , Nature , Nature Physics
© 2014 Phys.org