Improving methods used to analyze and model fluid dynamics

Understanding how fluids flow and the forces that affect them at various scales and boundary conditions (e.g., flat or curved flow domain boundaries) is relevant to solving a host of physics problems that impact diverse research in both the scientific and industrial sectors.

To improve the numerical methods and algorithms used to analyze and model physical phenomena associated with fluid flows, scientists from Pacific Northwest National Laboratory and the University of South Florida demonstrated the viability of a new method: smoothed particle hydrodynamics-continuous boundary force, or SPH-CBF. Their novel CBF method solves Navier-Stokes equations (used to describe fluid motion) subjected to Robin boundary conditions using an SPH method for solving partial differential equations. Their SPH-CBF formulation has several advantages for solving Navier-Stokes equations. Most notably, the SPH discretization of the equations and boundary condition that results from the CBF method offer a computationally efficient way to model boundary conditions ranging from no slip, where the fluid matches the surface velocity, to full slip.

While ongoing work in computational fluid dynamics continues to improve the calculations required to simulate interactions of liquids and gases with surfaces defined by boundary conditions, not all of these processes are straightforward to implement or even accurate. For SPH, an accurate implementation of no- or partial-slip boundary conditions for Navier-Stokes equations has been elusive because the kernels used in interpolation are incomplete near boundaries, forcing researchers to employ methods such as placing mirror or ghost particles across the boundary from the fluid particles. These methods can be correct, but they are difficult to implement in three-dimensional domains bounded by complex boundaries (e.g., sharp corners). With this new method for solving Navier-Stokes equations subjected to Robin boundary conditions, researchers are providing a significant advancement to existing SPH theory. The SPH-CBF formulation also takes advantage of smoothed particle hydrodynamics strengths in modeling diverse physical problems, including those involving atmospheric systems, energy materials and processes, subsurface flow and transport, and high-strength materials-all of which are relevant to important U.S. Department of Energy (DOE) mission objectives.

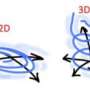
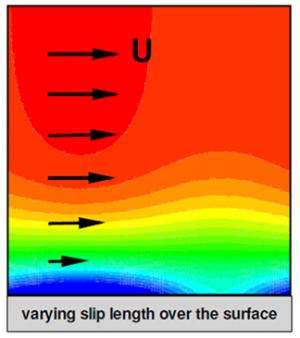
In the CBF method, the Robin boundary condition is replaced by a homogeneous Neumann boundary condition and a source term is added into the Navier-Stokes equations. While direct implementation of a Robin boundary condition in SPH is a challenge, the homogeneous Neumann boundary condition can be implemented and discretization (i.e., converting continuous space into discrete, or finite, space for simpler calculation) of the added force term completed relatively easily with smoothed particle hydrodynamics. To examine accuracy, the SPH-CBF method was tested with a two-dimensional (2-D) plane shear flow with the Navier slip condition at the lower boundary, a flow through a periodic lattice of cylinders with the Navier slip condition at each cylinder's surface, and a 2-D plane shear flow with a space-dependent Robin boundary condition at the lower boundary that was further extended to three spatial dimensions. Then, the results were compared with those obtained using finite difference or finite element method (FEM) approaches. Even in a domain with complex boundaries, comparisons of SPH-CBF velocity profiles closely agreed with those obtained from the FEM solutions, demonstrating the method's capability for modeling flows with different slip lengths.

This work contributes to ongoing efforts involving particle-based and continuum-scale mathematical methods being conducted as part of the Collaboratory on Mathematics for Mesoscopic Modeling of Materials, or CM4, project. CM4 is focused on developing mathematical foundations for understanding and controlling fundamental mechanisms in mesoscale processes to enable scalable synthesis of complex materials via the design of efficient modeling methods and corresponding scalable algorithms.