Engineers gain insight into turbulence formation and evolution in fluids
in the patterns that natural gas makes as it swirls through a transcontinental pipeline or in the drag that occurs as a plane soars through the sky. Reducing such turbulence on say, an airplane wing, would cut down on the amount of power the plane has to put out just to get through the air, thereby saving fuel. But in order to reduce turbulence—a very complicated phenomenon—you need to understand it, a task that has proven to be quite a challenge.
Since 2006, Beverley McKeon, professor of aeronautics and associate director of the Graduate Aerospace Laboratories at the California Institute of Technology (Caltech) and collaborator Ati Sharma, a senior lecturer in aerodynamics and flight mechanics at the University of Southampton in the U.K., have been working together to build models of turbulent flow. Recently, they developed a new and improved way of looking at the composition of turbulence near walls, the type of flow that dominates our everyday life.
Their research could lead to significant fuel savings, as a large amount of energy is consumed by ships and planes, for example, to counteract turbulence-induced drag. Finding a way to reduce that turbulence by 30 percent would save the global economy billions of dollars in fuel costs and associated emissions annually, says McKeon, a coauthor of a study describing the new method published online in the Journal of Fluid Mechanics on July 8.
"This kind of turbulence is responsible for a large amount of the fuel that is burned to move humans, freight, and fluids such as water, oil, and natural gas, around the world," she says. "[Caltech physicist Richard] Feynman described turbulence as 'one of the last unsolved problems of classical physics,' so it is also a major academic challenge."
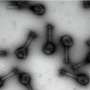
Wall turbulence develops when fluids—liquid or gas—flow past solid surfaces at anything but the slowest flow rates. Progress in understanding and controlling wall turbulence has been somewhat incremental because of the massive range of scales of motion involved—from the width of a human hair to the height of a multi-floor building in relative terms—says McKeon, who has been studying turbulence for 16 years. Her latest work, however, now provides a way of analyzing a large-scale flow by breaking it down into discrete, more easily analyzed bits.
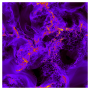
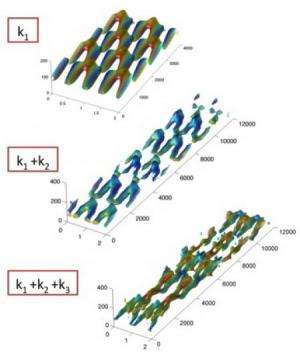
McKeon and Sharma devised a new method of looking at wall turbulence by reformulating the equations that govern the motion of fluids—called the Navier-Stokes equations—into an infinite set of smaller, simpler subequations, or "blocks," with the characteristic that they can be simply added together to introduce more complexity and eventually get back to the full equations. But the benefit comes in what can be learned without needing the complexity of the full equations. Calling the results from analysis of each one of those blocks a "response mode," the researchers have shown that commonly observed features of wall turbulence can be explained by superposing, or adding together, a very small number of these response modes, even as few as three.
In 2010, McKeon and Sharma showed that analysis of these blocks can be used to reproduce some of the characteristics of the velocity field, like the tendency of wall turbulence to favor eddies of certain sizes and distributions. Now, the researchers also are using the method to capture coherent vortical structure, caused by the interaction of distinct, horseshoe-shaped spinning motions that occur in turbulent flow. Increasing the number of blocks included in an analysis increases the complexity with which the vortices are woven together, McKeon says. With very few blocks, things look a lot like the results of an extremely expensive, real-flow simulation or a full laboratory experiment, she says, but the mathematics are simple enough to be performed, mode-by-mode, on a laptop computer.
"We now have a low-cost way of looking at the 'skeleton' of wall turbulence," says McKeon, explaining that similar previous experiments required the use of a supercomputer. "It was surprising to find that turbulence condenses to these essential building blocks so easily. It's almost like discovering a lens that you can use to focus in on particular patterns in turbulence."
Using this lens helps to reduce the complexity of what the engineers are trying to understand, giving them a template that can be used to try to visually—and mathematically—identify order from flows that may appear to be chaotic, she says. Scientists had proposed the existence of some of the patterns based on observations of real flows; using the new technique, these patterns now can be derived mathematically from the governing equations, allowing researchers to verify previous models of how turbulence works and improve upon those ideas.
Understanding how the formulation can capture the skeleton of turbulence, McKeon says, will allow the researchers to modify turbulence in order to control flow and, for example, reduce drag or noise.
"Imagine being able to shape not just an aircraft wing but the characteristics of the turbulence in the flow over it to optimize aircraft performance," she says. "It opens the doors for entirely new capabilities in vehicle performance that may reduce the consumption of even renewable or non-fossil fuels."
Provided by California Institute of Technology