June 14, 2013 report
Researchers prove quantum algorithm works by solving linear equations on a quantum computer
(Phys.org) —A research team composed of members from China, Singapore and Canada has built a simple quantum computer that has proven a quantum algorithm developed in 2009. In their paper published in Physical Review Letters, the team describes how they built their simple quantum computer and how it might be developed into a more powerful machine.
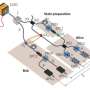
As scientists continue their quest to build a true quantum computer, they take baby steps by creating quantum-based devices capable of carrying out quantum algorithms. In this latest effort, the research team built a simple device that uses entangled photons to solve 2x2 linear equations.
Back in 2009, a team of researchers developed an algorithm that they believed could be used by a quantum computer to solve linear equations. To find out if that algorithm truly would work as proposed, the research team built a simple quantum device to run it. They started by firing a laser beam at barium-borate crystals to create two pairs of entangled photons—each of the pairs had the same polarization. The photon pairs were then sent through a beam splitter that separated them from the others. The four photons were used to represent qubits which were processed by an optical circuit. Afterwards, the photons were detected by a sensor—their polarization state represented the solution to the linear equations given at the onset. The device doesn't give an exact answer, but instead provides what it's most likely to be. In this case, the algorithm developed in 2009 proved to be reasonably accurate, providing fidelity of 0.993 to 0.825.
The simple device created by the team demonstrates the working principle of the algorithm, and opens the door to solving much larger equations by upping the number of entangled photons. Its creation also suggests that similar devices could be created to solve different types of equations. The team points out that that there are two elements of their device they would like to improve. The first is that it's limited by use of just one photon source. That makes the creation of the photons somewhat unreliable. They'd also like to find a way to implement more efficient photon detectors.
More information: Experimental Quantum Computing to Solve Systems of Linear Equations, Phys. Rev. Lett. 110, 230501 (2013) prl.aps.org/abstract/PRL/v110/i23/e230501
Abstract
Solving linear systems of equations is ubiquitous in all areas of science and engineering. With rapidly growing data sets, such a task can be intractable for classical computers, as the best known classical algorithms require a time proportional to the number of variables N. A recently proposed quantum algorithm shows that quantum computers could solve linear systems in a time scale of order log (N), giving an exponential speedup over classical computers. Here we realize the simplest instance of this algorithm, solving 2×2 linear equations for various input vectors on a quantum computer. We use four quantum bits and four controlled logic gates to implement every subroutine required, demonstrating the working principle of this algorithm.
Journal information: Physical Review Letters
© 2013 Phys.org











.jpg)