April 2, 2013 report
Phase transition may explain how brain neurons encode information
(Phys.org) —While scientists know that information is represented in the brain by the electrical activity of neurons, the details of this representation, called "neural coding," remain mysterious. How exactly do pulses of electricity get translated into thoughts and ideas?
In the standard model of neuronal firing, neurons can use two kinds of neural codes: rate codes, in which information is encoded only in the average rate of firing; and temporal codes, in which information is encoded not only in the average rate but also in the precise timing of each pulse, with sensitivity down to the submillisecond range. Temporal firing means that firing patterns with the same average rate can encode different messages—a key insight into understanding neural coding. While the distinction between the two neural codes has previously been considered one of degree, a new study has found that neurons change between the two coding regimes abruptly rather than smoothly due to a phase transition separating the two regimes.
The researchers, Thibaud Taillefumier and Marcelo Magnasco at The Rockefeller University in New York, have published their paper on their discovery of a neural phase transition in a recent issue of PNAS.
"Just like a phase transition between a solid and a liquid allows us to make a clear distinction between the two phases of matter, we discovered that there is also a phase transition between rate codes and temporal codes in neural coding, and this distinction remains even when you are not considering a theoretical model but actual liquids/solids, with imperfections or impurities," Magnasco told Phys.org.
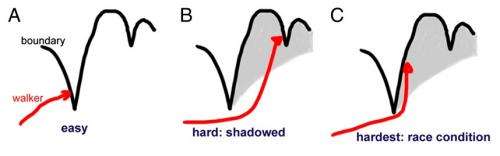
The researchers' discovery of the phase transition between the two neural regimes arises from a more general mathematical question called the "first passage problem." The question is, when is the first time that a fluctuating quantity (e.g., voltages in neurons, prices in a market, etc.) reaches a given boundary? The question becomes even more difficult when the boundary itself is fluctuating—as is often the case in real-life situations, including the neural coding scenario.
In neural coding, neurons generate electrical pulses, or action potentials, to encode information and communicate with each other. In order for a neuron to generate one of these pulses, its membrane voltage must exceed a threshold voltage, which then triggers a chain reaction of events in the neuron that ultimately causes it to fire. The neuron's membrane voltage is constantly fluctuating in response to both electrical pulse inputs from other neurons as well as the neuron's own internal noise. The threshold voltage also fluctuates, so that at certain times the neuron's membrane must have more voltage to surpass the threshold than at other times.
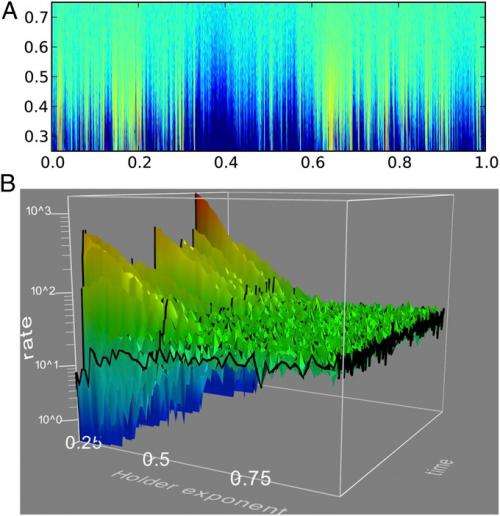
In this study, the researchers investigated the probability that a neuron's fluctuating membrane voltage first exceeds the fluctuating threshold, and found that this probability undergoes a phase transition as a function of the roughness of the boundary, which refers to how much the threshold boundary fluctuates.
The researchers mathematically defined boundary roughness by the Holder exponent, H. The boundary is perfectly smooth at H = 1. The researchers identified the critical value at which the phase transition occurs at H = ½, the point at which the roughness of the fluctuating boundary equals the roughness of the fluctuating quantity. They found that, when H > ½ (smoother boundary), the probability density for finding the "first passage" of the fluctuating quantity through the fluctuating boundary is a continuous function. That is, the probability is never zero and never infinity, but always somewhere in between. When H < ½ (rougher boundary), the opposite abruptly occurs: the probability density is everywhere either zero or infinity. In mathematical terms, it ceases to be a function and becomes divergent.
Although the finding of a phase transition at H = ½ is a general finding that can be applied to many areas, it is particularly relevant in the case of neural coding. Previous research in neural coding has shown that, when H = ½, a neuron's input voltage is uncorrelated yet precisely balanced; in other words, it is white noise.
"If you plot the fluctuating voltage of the neural membrane as a function of time, it has a value of H = ½," Magnasco said. "What our calculation shows is that, at least mathematically, the trajectory with the smallest H always wins—when the walker has the lowest H, then it can always overtake the boundary, while when it is the boundary with the smallest H then when the walker starts from behind it has zero chances of catching up—until the boundary reverses on itself and turns back down."
This significance of H = ½ in neural coding led the researchers to realize that the phase transition at this value defines a sharp boundary between rate codes (which occur with a smoother boundary, when H > ½) and temporal codes (which occur with a rougher boundary, when H < ½). An individual neuron can switch back and forth between rate coding and temporal coding depending on its input characteristics and the threshold boundary roughness. Temporal codes in particular are thought to play an important role in early auditory coding and motor coding.
Because the first passage problem appears in many situations, the discovery of the phase transition may have implications for diverse areas such as voltages in electrical circuits, prices of commodities in markets, the variables describing the severity of a disease, the time-to-failure of a device, game theory problems, and biological species extinction probabilities, among others.
In the future, the researchers want to further investigate the implications of boundary roughness.
"We want to understand if there is a single 'timing' regime or whether there are multiple regimes for different H < ½," Magnasco said. "We also are carrying out simulations in large networks to learn how the effective value of H observed by any given neuron depends as a function of network organization."
More information:
Thibaud Taillefumier and Marcelo O. Magnasco. "A phase transition in the first passage of a Brownian process through a fluctuating boundary with implications for neural coding." PNAS Early Edition. DOI: 10.1073/pnas.1212479110
Also at arXiv:1206.6129 [q-bio.NC]
Journal information: Proceedings of the National Academy of Sciences
© 2013 Phys.org