March 7, 2013 feature
Through a sensor, clearly: Complex systems made observable
(Phys.org) —A complex system can, in principle, be observable – that is, the system's complete internal state can be reconstructed from its outputs, which would ostensibly involve describing in complete quantitative detail all of its internal state variables at once. In an actual experiment, however, such measurement is typically beyond our reach, and so is limited to a smaller number of those variables. Referred to as sensors (or sensor nodes), these key variables can be used to make the complete system observable. Recently, scientists at Northeastern University and MIT devised a graphical approach that first derives the mathematical equations describing a complex system's dynamics, and then determines the key sensors for that system. Moreover, when applying their approach to biochemical reaction systems, the researchers discovered that the derived sensors were both necessary and sufficient to describe the complete system. The scientists conclude that their findings allow a systematic exploration of many diverse natural, technological and socioeconomic systems.
Dr. Yang-Yu Liu comments on the research he, Prof. Albert-László Barabási and Prof. Jean-Jacques Slotine performed, starting with the three main challenges they faced. "The primary challenge is that for many nonlinear systems, we don't know the system parameters," Liu tells Phys.org. "However, conceptually it is quite straightforward to adopt a graphical approach derived from the dynamical laws that govern a system to determine the sensors that are necessary to reconstruct the full internal state of a complex system."
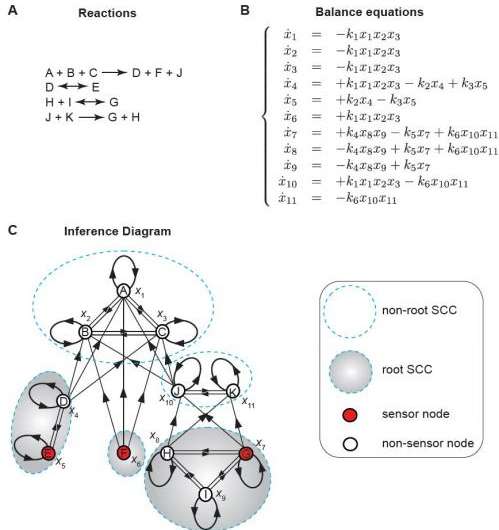
In fact, control theorists have been working on the concept of system digraphs some time. Liu and his associates used this approach to study the observability problem for highly nonlinear systems, which he says that to his knowledge has not been previously addressed. "The surprise," Liu adds, "was that, except for some pathological cases which almost never occur in real systems, the sensors we identified are not only necessary but also sufficient: Usually, we expect that to observe the system we'd need to monitor more sensors than just the necessary nodes, since if the topology of a dynamic system's inference diagram is very complex, it's hard to have any symmetries. However, the complicated topology somehow helped us achieve system observability." An inference diagram reveals the underlying structure of information flow or casualty when the measurements are performed.
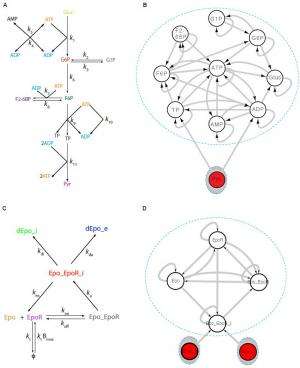
Lastly, Liu addressed the challenge of reconstructing selected state variables from appropriately chosen outputs using their graphical approach. "The reconstruction of other state variables is highly nontrivial task," Liu explains. This is the so-called observer design problem, which can be defined as the problem of designing observers which are insensitive to nonlinear behavior, sensor noise, modeling errors, and other effects. "For biochemical reaction systems, or any general nonlinear systems, the observer design problem is very difficult. In this paper, we were concerned only with observability, rather than the observer design."
Since the team's graphical approach relies only on the dynamics equations, notes Liu, their findings offer avenues to systematically explore the dynamics of a wide range of natural, technological and socioeconomic systems. "For any nonlinear systems, as long as we can come up with a suitable set of nonlinear dynamic equations, we should be able to construct the inference diagram. We can then use strongly connected component, or SCC, analysis to get the necessary sensors that need to be monitored. This approach is applicable to any nonlinear system."
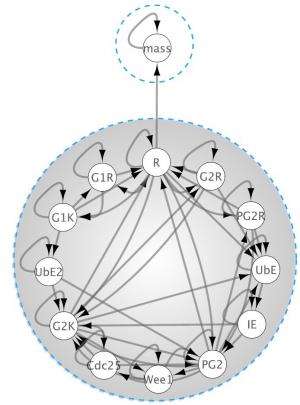
This idea alone is tremendously important, since the statistical rules describing different classes of complex systems (for example, biological systems vs. large-city urbanization) vary significantly. However, to address the observability problem Liu and his colleagues propose a general framework – so once the complex system's dynamics equations are derived, the inference diagram can be constructed and the key sensors identified. "For example," Liu illustrates, "in addition to the biological systems discussed in our paper, one can apply this approach to social dynamic system such as opinion or social influence dynamics. "
Moving forward, Liu describes other innovations the researchers might develop and apply to the current experimental design. "We may want to also infer all system parameters, which can be viewed as a special type of state variables with time derivative 0. This is a rather challenging question, but without knowing the system parameters, we can never design a real observer to completely construct the system's internal state. We'd also like to get more biological implications and applications from the biological systems sensors we identified."
More information: Observability of complex systems, PNAS February 12, 2013 vol. 110 no. 7 2460-2465, doi:10.1073/pnas.1215508110
Journal information: Proceedings of the National Academy of Sciences
Copyright 2013 Phys.org
All rights reserved. This material may not be published, broadcast, rewritten or redistributed in whole or part without the express written permission of Phys.org.