September 18, 2012 report
Dark matter effect might be explained by modified way to calculate inertial mass
(Phys.org)—One of the first observations suggesting the existence of an invisible dark matter came in 1933 when astronomer Fritz Zwicky noticed that galaxy clusters were more energetic than they should be, according to the mass of visible stars in them, and he proposed dark matter to explain the discrepancy. Later observations of galaxies (by Rubin & Ford, among others) showed that the galaxies' edges were rotating as fast as the insides of the galaxies, even though acceleration is supposed to decrease with radius.
While dark matter is still the most popular explanation for this and other problems, there have also been many proposed alternative explanations. Most recently, Michael McCulloch of Plymouth University in the UK, who specializes in geomatics (the mathematics of positioning in space), has proposed that a new model that modifies a galaxy's inertial mass may account for the faster-than-expected rotation at a galaxy's outer edges, even though this model violates Einstein's famous equivalence principle.
McCulloch's paper on the model of modified inertial mass is published in Astrophysics and Space Science, and is also posted at arXiv.org.
Two kinds of mass
In general, there are two ways to calculate the mass of any object. One way involves comparing the force of gravity on an object of unknown mass to the force of gravity on an object whose mass is known. This method, which the bathroom scale is based on, gives an object's gravitational mass. The second method, which gives inertial mass, involves applying a known force to an object of unknown mass, measuring the resulting acceleration, and calculating the mass using Newton's Second Law (m = F/a).
In 1907, Einstein proposed that gravitational mass and inertial mass are always equal, which is known as the equivalence principle and serves as a fundamental concept of general relativity. Although tests of the equivalence principle have verified that Einstein is correct to many decimal places of accuracy, some scientists have been willing to violate the equivalence principle in attempts to explain the galactic rotation problem without invoking dark energy.
One such explanation came in 1983, when physicist Mordehai Milgrom proposed a theory called Modified Newtonian Dynamics (MoND) that can either slightly modify the gravitational constant or slightly modify Newston's second (inertial) law at very small gravitational accelerations. According to MoND, the velocity of stars in a circular orbit far from the center of a galaxy is a constant and does not depend on the distance from the center. However, for MOND to work, an adjustable parameter must be set.
In 2007, McCulloch proposed a model to explain the flatness of galactic rotation that is similar to the second (inertial) version of MoND in that it also proposes modifications of an object's inertial mass at small accelerations, deviating from Newton's second law. Unlike MOND, this new model does not need an adjustable parameter. However, both models violate the equivalence principle when masses have very small accelerations – and at the edges of galaxies, the gravitational acceleration is extremely small compared to that on Earth.
"The accelerations we are familiar with on Earth are around 9.8 m/s2," McCulloch told Phys.org. "At the edges of galaxies, the acceleration is only on the order of 10-10 m/s2. At this tiny acceleration it would take you 317 years to get from rest to a speed of 1 m/s, or from 0 to 60 miles per hour in 8500 years! Or, as Milgrom once wrote, the lifetime of the universe to get near to the speed of light."
Mass of accelerating objects
In the new study, McCulloch expands on his model, called Modification of Inertia resulting from a Hubble-scale Casimir effect (MiHsC), or Quantized Inertia. This model proposes that accurately calculating an object's inertial mass involves accounting for the emission of photons, or Unruh radiation, that occurs as a result of the object's acceleration with respect to surrounding matter. The existence of Unruh radiation is a subject of some dispute, since it is unclear whether it has been observed.
In the MiHsC model, a Hubble-scale Casimir effect, which can be thought of as a vacuum energy arising from virtual particles, imposes restrictions on the Unruh radiation wavelengths. As an object's acceleration decreases, Unruh wavelengths lengthen to the Hubble scale, and more of them are disallowed. Because this radiation is assumed in MiHsC to contribute to inertial mass, a decrease in acceleration leads to fewer Unruh waves and a gradual decrease in the object's inertial mass. With a smaller inertial mass, a star within a galaxy can be accelerated into a bound orbit more easily by the same gravitational force.
"There are two kinds of mass: gravitational mass (GM, measured by the gravitational force produced by the galaxy) and inertial mass (IM, measured by the ease of response of a star to a force)," McCulloch said. "These are usually assumed to be equal. The point is that you can either (1) increase the GM of the galaxy to hold its stars in with more force (dark matter), or (2) you can decrease the IM of the stars so that they can be bent more easily into a bound orbit even by the small existing gravitational force from the visible mass. MiHsC/quantized inertia does the latter."
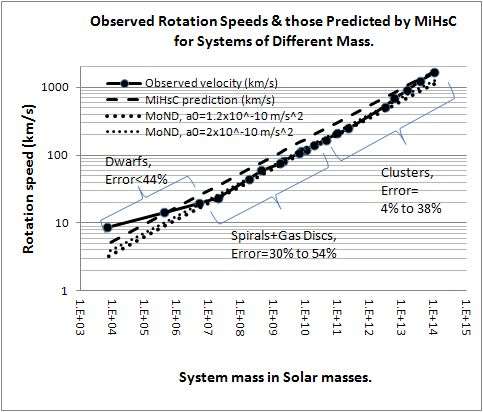
By assuming that a galaxy's inertia is due to Unruh radiation that is subject to a Hubble-scale Casimir effect, McCulloch derived a relation between the velocity and visible mass of a galaxy or galaxy cluster (a Tully-Fisher relation). Using only the mass from baryonic (visible) matter, he could use the relation to predict the rotational velocity of dwarf galaxies, spiral galaxies, and galaxy clusters. Although the predictions overestimate the observed velocities by one-third to one-half, they are still within error bars. (Uncertainty arises from uncertainty in the Hubble constant and in the ratio of stellar mass to light, affecting mass estimates based on observation.)
"MiHsC predicts that, as an object's acceleration decreases, the Unruh waves it sees become large compared to the Hubble scale, so they become impossible to detect and so a greater proportion of them are disallowed," McCulloch explained. "This kind of thinking, 'If you can't directly observe it, then forget it,' may seem strange, but it has a distinguished history. It was discussed by Berkeley and Mach, and it was used by Einstein to discredit Newton's concept of absolute space and formulate special relativity. Back to MiHsC: at this low acceleration then, stars cannot see the Unruh waves, start to lose their inertial mass very quickly, and this makes it easier for an existing external force to accelerate them again, so their acceleration increases, they see more Unruh waves, gain inertia and decelerate. A balance is achieved around a minimum acceleration which is predicted to be close to the recently observed cosmic acceleration, and MiHsC predicts galaxy rotation within the uncertainty without any adjustable parameters."
Although MiHsC and MoND are somewhat similar, as mentioned above, with both predicting the observed velocities within error bars, MiHsC uses no adjustable parameters while MoND requires an unexplained adjustable acceleration parameter to fit the data.
Testing predictions
Whether or not MiHsC turns out to be true remains to be seen. As noted above, the model violates Einstein's equivalence principle. Although the equivalence principle has been well tested, this particular violation of it could not have been seen in those tests.
"At the normal accelerations that we see on Earth (9.8 m/s2), the disagreement between MiHsC and equivalence is tiny; it only becomes important at accelerations as small as 10-10 m/s2," McCulloch said. "Torsion balance experiments have tested the equivalence principle down to accelerations of 10-15 m/s2, but they cannot show the effects of MiHsC. This is because these experiments are more accurate versions of Galileo's experiment in which he dropped two objects of different mass off a tower. If the equivalence principle is right the heavier object should be attracted downwards (gravitationally) more to the Earth (due to its greater gravitational mass, GM), but also find it equally harder to accelerate towards the Earth due to its greater inertial mass (IM), so the two objects should fall together. The anomalous acceleration predicted by MiHsC due to the difference between GM and IM is independent of the mass of the objects, so the two objects would still drop together, although both would drop slightly more quickly than expected. So, MiHsC cannot be detected in these kinds of experiments."
Also, MiHsC makes a testable prediction, which is that accelerations at a galaxy's edge should remain above a certain value to offset the traditional decrease in acceleration with radius. McCulloch hopes that future observations will provide support for the MiHsC model.
"I am trying to devise an unambiguous test," he said. "The problem with astronomical data is that often there can be more than one explanation of an observation, so it is hard to prove things conclusively. The best proof would be a lab experiment where one can control the conditions and isolate causes. A possible experiment would be to cool an object to say 5K while weighing it. Tests with spacecraft may also be possible. I am trying to get funding to attempt something like this."
More information:
M.E. McCulloch. "Testing Quantised Inertia on Galactic Scales." Astrophysics and Space Science. DOI: 10.1007/s10509-012-1197-0
Also at arXiv:1207.7007v1 [physics.gen-ph]
McCulloch's blog: http://physicsfromtheedge.blogspot.co.uk/
Journal information: Astrophysics and Space Science
© 2012 Phys.org