April 7, 2024 feature
This article has been reviewed according to Science X's editorial process and policies. Editors have highlighted the following attributes while ensuring the content's credibility:
fact-checked
peer-reviewed publication
trusted source
proofread
Scientists investigate information propagation in interacting bosonic systems
A new study by scientists from Japan explores the propagation of quantum information within interacting boson systems like Bose-Einstein condensates (BECs), revealing the potential for accelerated transmission unlike previously thought.
Quantum many-body systems, like interacting boson systems, are fundamentally important as they find applications in various branches of physics. The propagation of information in quantum many-body systems is governed by the Lieb-Robinson bound. This quantifies how quickly information or changes propagate through a quantum system.
When you make a change in one part of the system, the Lieb-Robinson bound describes the speed at which this change influences other parts of the system. In practical terms, it means that the effect of your initial change will spread outwards from its point of origin, affecting neighboring regions of the system.
However, the Lieb-Robinson bound for interacting boson systems has long remained a challenge.
The researchers, led by Dr. Tomotaka Kuwahara, the RIKEN Hakubi Team Leader at the RIKEN Center for Quantum Computing, address this challenge in their new Nature Communications study.
Dr. Kuwahara explained the importance of their work to Phys.org, highlighting the importance of understanding quantum systems containing fundamental particles like bosons and fermions.
"The boson systems have, in principle, no energy limit, which made the Lieb-Robinson bound in bosonic systems significantly challenging," he said.
The Lieb-Robinson bound
As mentioned earlier, the Lieb-Robinson bound provides a quantitative limit on how quickly correlations or influences can spread between spatially separated regions of a quantum system.
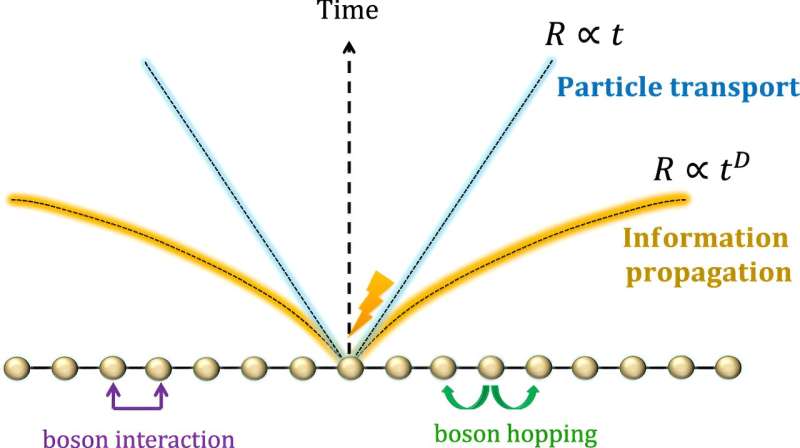
What this means is that the propagation cannot be instantly everywhere and instead is limited to an effective light cone. Inspired by Einstein's theory of relativity, the light cone represents all points in space and time that a light signal emitted from an event can reach. This creates a double cone: one for the past and one for the future.
The same applies to information propagation in quantum many-body systems, i.e., systems with more than two quantum particles.
"The Lieb-Robinson bound sets a universal speed limit for how quickly information can travel in these systems," explained Dr. Kuwahara.
According to the Lieb-Robinson bound, the propagation of information is limited and decays exponentially with distance or time. The specifics of the decay depend on the individual system and the interactions that can occur within the system.
Formulated by Elliott Lieb and Derek Robinson in 1972, the Lieb-Robinson bound is only applicable for non-relativistic systems, which is to say that the information is traveling at speeds much less than the speed of light.
The Bose-Hubbard model
Interacting boson systems consist of many bosons (like photons). These systems, while common, present many challenges, such as long-range interactions between bosons and unbounded energy, making it hard to develop simulations and theoretical models.
But, since the discovery of the BEC, models such as the Bose-Hubbard model have been developed to study bosonic systems. The Bose-Hubbard model is a theoretical framework used to understand how bosons behave when confined to a lattice structure, like atoms in a crystal.
This model takes into account two main factors. First is the hopping of bosons from one lattice site to another, represented by the hopping parameter. Second is the on-site interaction parameter, representing the repulsive forces between bosons when they occupy the same site. This interaction energy increases as more bosons occupy the same site.
These factors incorporate the interaction between the bosons, which is why the researchers chose the Bose-Hubbard model to investigate the Lieb-Robinson bounds in interacting boson systems.
The upper limits
The researchers chose to study the Lieb-Robinson bound for a D-dimensional lattice (interacting boson system) governed by the Bose-Hubbard model. They found three results for this system.
Result 1
This result addresses the interaction of bosons within the lattice. The researchers found that the speed of boson transport is limited, even in systems with long-range interactions. This speed, though limited, does grow at most logarithmically with time, which is relatively slow.
This finding provides crucial insights into the dynamics of boson systems, putting an upper bound on its speed.
Result 2
This result focuses on the propagation of operators of the system over time. Operators are basically variables of the system, like momentum. As these operators propagate, they deviate from the ideal evolution, leading to the accumulation of error.
This error propagation determines how fast information can propagate in the system. For example, if the error is large, it indicates that information propagation is slower or more constrained, as the approximation deviates significantly from the ideal evolution of the system.
Similarly, if the error is small, then information propagation is fast. This aligns with the Lieb-Robinson bound, indicating the presence of an upper bound on error propagation.
Despite the presence of an upper bound on error propagation, interactions among bosons induce clustering in specific regions. These regions, characterized by higher boson concentrations, facilitate accelerated information propagation along certain lattice paths or directions.
This phenomenon aligns with the Lieb-Robinson bound. However, this acceleration is bounded and has a polynomial growth depending on the dimensionality of the system.
Result 3
This result presents a way for simulating these systems using elementary quantum gates (like CNOT). The researchers provide an upper bound on the number of elementary quantum gates required for efficiently simulating the time evolution of interacting boson systems.
Comparison with fermionic systems
Fermionic systems show a finite speed limit for how fast information can propagate. Before this work, scientists assumed the same for bosonic systems, which is untrue.
"The light cone spreads out much faster and is non-linear, i.e., speeds up over time. Specifically, if you're looking at a three-dimensional space, the distance 'information' can travel grows with the square of the time. So, in this sense, bosons can send information much faster than fermions can, especially as time goes on," explained Dr. Kuwahara.
This depends on the number of bosons that can occupy the same state at the same time. Essentially, the more bosons that join in, the faster information can propagate.
"But, since bosons can only move with a finite speed, it takes a bit of time for a lot of them to get together, leading to a limited speed of information propagation. Over time, as more bosons cooperate, the speed at which they can send information goes up," said Dr. Kuwahara.
This work opens a new window into exploring interacting boson systems for information propagation.
"I anticipate that the algorithm will be used to simulate condensed matter physics, which could lead to the discovery of new quantum phases. It should also prove useful in simulating quantum thermalization, helping to tackle the basic question of how closed quantum systems settle into a steady state over time," concluded Dr. Kuwahara.
More information: Tomotaka Kuwahara et al, Effective light cone and digital quantum simulation of interacting bosons, Nature Communications (2024). DOI: 10.1038/s41467-024-46501-7.
Journal information: Nature Communications
© 2024 Science X Network