Computing how quantum states overlap

Quantum many-body systems are things such as atomic nuclei that consist of many tiny particles moving in complex ways. This makes it extremely difficult to predict how the systems behave as the particles interact. To study these systems, researchers use computational tools called quantum Monte Carlo simulations.

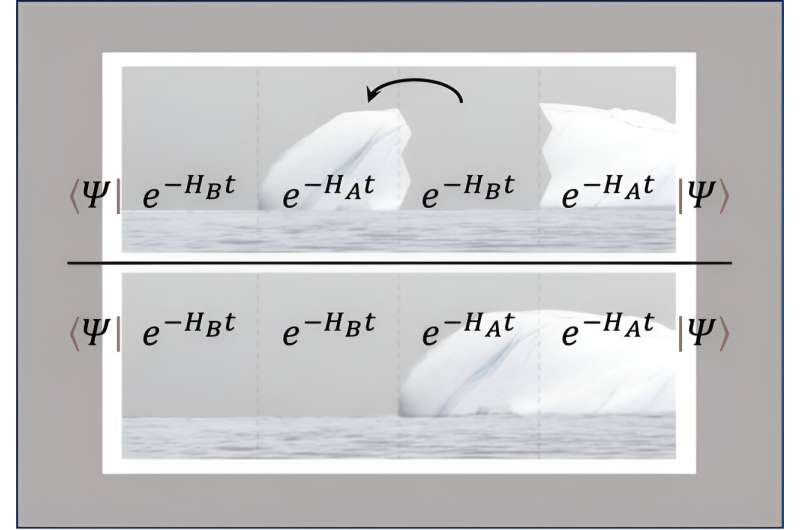
In this work, researchers used a specific quantum Monte Carlo approach called the "floating block method" to compute atomic nuclei corresponding to two different Hamiltonians and how they overlap. Hamiltonians are mathematical descriptions of the energy of a quantum system. The study is published in the journal Physical Review Letters.

Studying Hamiltonians allows scientists to understand how a quantum system changes over time. The floating block method makes it feasible to make calculations that were previously impossible for large quantum systems.

The floating block method allows researchers to use quantum Monte Carlo simulations to build fast and accurate emulators for quantum systems. It works by computing data for several different specific parameter values—the values that define the quantum system.

These baseline data allow researchers to create an emulator that will accurately predict the results for all parameter values in a specific range. This use of the floating block method and quantum Monte Carlo simulations has many potential applications. For example, it could aid scientists working on quantum computing.

Researchers from Forschungszentrum Jülich, the University of Bonn, and the Facility for Rare Isotope Beams at Michigan State University used the floating block method to compute the overlap between energy states of different Hamiltonians using quantum Monte Carlo calculations.

To compute the overlap between energy states, the floating block method uses imaginary (as opposed to real-valued) time evolution for two different Hamiltonians and rearranges the time blocks in a gradual sequence of calculations. The process is reminiscent of a block of ice breaking away from a large ice mass and floating into the sea.

The computational efficiency of the floating block method is orders of magnitude better than other approaches, with the computational advantage growing even larger with system size.