A method to compute the Rényi entanglement entropy in auxiliary-field quantum Monte Carlo simulations

Entanglement is a widely studied quantum physics phenomenon, in which two particles become linked in such a way that the state of one affects the state of another, irrespective of the distance between them. When studying systems comprised of several strongly interacting particles (i.e., many body systems) in two or more dimensions, numerically predicting the amount of information shared between these particles, a measure known as entanglement entropy (EE), becomes highly challenging.

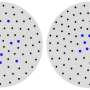
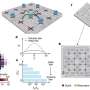
Researchers at Donostia International Physics Center recently introduced a new method to compute a measure of EE, namely the Rényi EE, for many-body systems beyond the reach of previous numerical methods. This method, outlined in Physical Review Letters, was effectively used to extract the universal features of EE in a 2D model of interacting fermions, focusing on the half-filled honeycomb Hubbard model.

"My previous research dealt with simple lattice models of quantum magnets, where I developed a highly efficient way of computing entanglement entropies on very large scales," Jonathan D'Emidio, lead author of the paper, told Phys.org. "Several years ago, I was asked by an expert in the field if it would be possible to apply this technique to more complicated models of fermions (electrons), where no adequate techniques were available."

D'Emidio started examining interacting fermion models in collaboration with his colleagues Román Orús, Nicolas Laflorencie and Fernando de Juan. Soon after they started collaborating on this project, the researchers realized that D'Emidio's previously developed computational method could also be effectively applied in this new context.

"The objective of our study was simple: to compute the Rényi EE in a model of interacting fermions with enough precision to see something interesting," D'Emidio said. "In particular, to observe features that can identify the various phases and phase transitions of the fermions. These features were predicted to exist but had never been directly observed in numerical simulations."

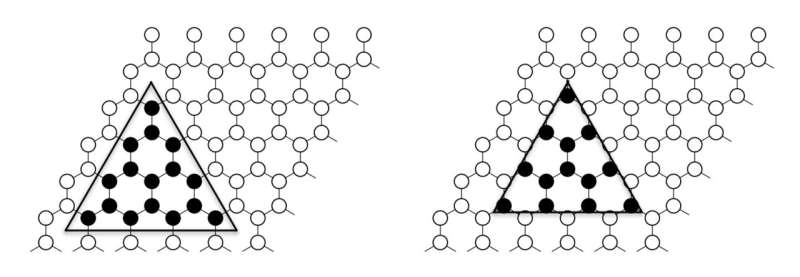
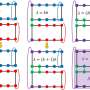
The method used by D'Emidio and his colleagues to compute the Rényi EE draws from basic concepts rooted in thermodynamics and statistical mechanics. Essentially, this method identifies the Rényi EE with a free-energy difference between two different fermion ensembles.

"As an example, free-energy differences tell you whether proteins will fold in a certain way, or if a certain reaction will occur naturally or not," D'Emidio explained. "To make these processes go in the opposite direction, one needs to perform work on the system. The original formulation that I used corresponded exactly to computing the work that is required to partially fuse together two copies of the quantum wave function."

The primary advantage of the computational technique proposed by this research team is that it naturally captures the most important configurations that dominate the overall EE value. This is in stark contrast with previous formulations, which suffered from the massive contributions of extremely rare events, making the associated calculations practically impossible to perform.

"One of the biggest surprises for us was that sometimes results can depend on how the entanglement region is defined, whereas theoretically there is no explanation for why this should be the case," D'Emidio said.

"For instance, when computing the EE of a triangle with the rest of the system, it should not matter how the triangle is placed on the lattice; yet we found the fingerprint of the phase transition was missed when the triangle had a zig-zag edge as opposed to a bearded edge. This result should hopefully help to gain a theoretical understanding of why the Rényi EE can depend on such definitions."

This recent study by D'Emidio and his collaborators demonstrates the feasibility of computing the Rényi EE with satisfactory precision, high enough to gather valuable new insight into the collective physics of systems comprised of interacting fermions. In their future works, the researchers plan to continue using their computational approach to study complex models of interacting many-body systems.

"I personally am very interested in studying spin-liquids, which are quantum phases that look completely disordered magnetically, but they actually have an intricate topological structure that can be revealed with properties of the EE," D'Emidio added.

"There are several spin-liquid candidates based on interacting fermion models, similar to the iconic Hubbard model that we investigated in this work. I would soon like to investigate these models with the new method."

© 2024 Science X Network