Physicists find signatures of highly entangled quantum matter
Via large-scale simulations on supercomputers, a research team from the Department of Physics, the University of Hong Kong (HKU), discovered clear evidence to characterize a highly entangled quantum matter phase—the quantum spin liquid (QSL), a phase of matter that remains disordered even at very low temperatures. This research has recently been published in npj Quantum Materials.
QSLs were proposed in 1973 by P. W. Anderson, the Nobel Physics Laureate of 1977. They have the potential to be used in topological quantum computing and to help understand the mechanisms of high-temperature superconductors that could greatly reduce energy costs during electricity transport owing to the absence of electrical resistance.
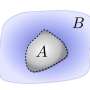
The QSL is called a liquid due to its lack of conventional order. QSLs have a topological order that originates from long-range and strong quantum entanglement. The detection of this topological order is a tough task due to the lack of materials that can perfectly achieve the many model systems that scientists propose to find a topological order of QSL and prove its existence. Thus, there has not been firmly accepted concrete evidence showing QSLs exist in nature.
Jiarui Zhao, Dr. Bin-Bin Chen, Dr. Zheng Yan, and Dr. Zi Yang Meng from HKU Department of Physics successfully probed this topological order in a phase of the Kagome lattice quantum spin model, which is a two-dimensional lattice model with intrinsic quantum entanglement and proposed by scientists that have Z2 (a cyclic group of order 2) topological order, via a carefully designed numerical experiment on supercomputers. Their unambiguous results of topological entanglement entropy strongly suggest the existence of QSLs in high entanglement quantum models from a numerical perspective.
"Our work takes advantage of the superior computing power of modern supercomputers, and we use them to simulate a very complicated model which is thought to possess topological order. With our findings, physicists are more confident that QSLs should exist in nature," said Jiarui Zhao, the first author of the journal paper and a Ph.D. student at the Department of Physics.
"Numerical simulations have been an important trend in scientific research of quantum materials. Our algorithms and computations could find more interesting and novel quantum matter and such efforts will surely contribute to the development of both practical quantum technology and the new paradigm in fundamental research," said Dr. Zi Yang Meng, Associate Professor in the Department of Physics.
The research
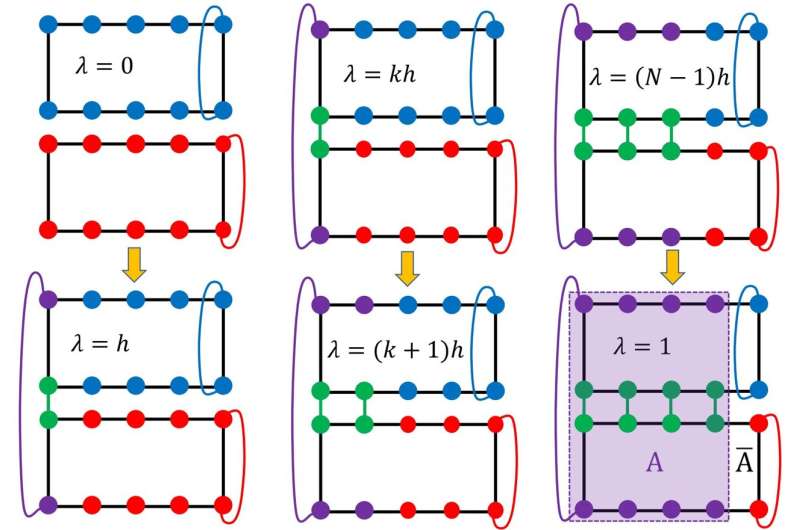
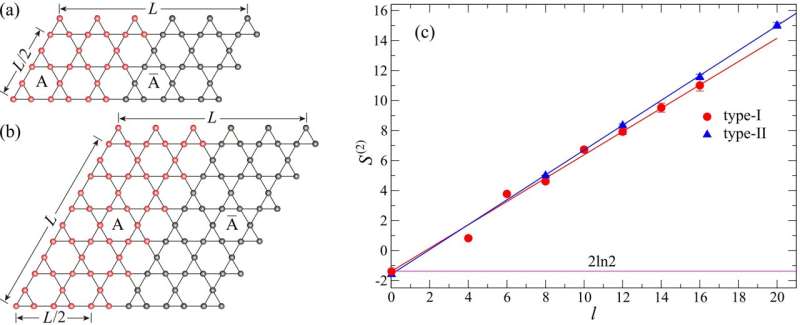
The team designed a numerical experiment on the Kagome spin model (Kagome is a two-dimensional lattice structure that shows a similar pattern to a traditional Japanese woven bamboo pattern in the shape of hexagonal latticework) in the proposed QSL phase, and the schematic plot of the experiment is illustrated in Figure 1. The entanglement entropy (S) of a system can be obtained by measuring the change of the free energy of the model during a carefully designed nonequilibrium process. The topological entropy (γ), which characterizes long-range topological order, can be extracted by subtracting the short-range contribution, which is proportional to the length of the entanglement boundary (l) from the total entanglement entropy(S), by fitting the data of entanglement entropy of different entanglement boundary length to a straight line (S=al-γ).
As shown in Figure 2, the team conducted the experiment on two kinds of lattices with different ratios of length and width to ensure the reliability of the results. The researchers used a straight line to fit the relation between the entanglement entropy with the length of the entanglement boundary so that the topological entropy should equal the intercept of the straight line. The results give the value of topological entropy to be 1.4(2), which is consistent with the predicted value of topological entropy of a Z2 quantum spin liquid, which is 2ln (2). The findings confirm the existence of QSLs from a numerical perspective.
More information: Jiarui Zhao et al, Measuring Rényi entanglement entropy with high efficiency and precision in quantum Monte Carlo simulations, npj Quantum Materials (2022). DOI: 10.1038/s41535-022-00476-0
Provided by The University of Hong Kong