This article has been reviewed according to Science X's editorial process and policies. Editors have highlighted the following attributes while ensuring the content's credibility:
fact-checked
peer-reviewed publication
trusted source
proofread
Trapped in the middle: Billiards with memory framework leads to mathematical questions
Adding one simple rule to an idealized game of billiards leads to a wealth of intriguing mathematical questions, as well as applications in the physics of living organisms. This week, researchers from the University of Amsterdam, including two masters' students as first authors—have published a paper in Physical Review Letters about the fascinating dynamics of billiards with memory.
An idealized version of the game of billiards has fascinated mathematicians for decades. The basic question is a simple one: Once a billiard ball is played, where does it go and where does it end up? Assume that the billiard is perfect: The walls are perfectly bouncy, there are no other objects on the table, the motion of the ball is frictionless, and so on. Then the ball will not really "end" anywhere; it will keep going forever.
But does it ever return where it started? Does it eventually visit every part of the table? When we slightly change the direction of the ball, or its starting location, does the path it follows look like the previous one?
All of these questions turn out to be very intriguing from a mathematical point of view. Their answers are not always known—especially when the shape of the billiard is not simple, like a square or a rectangle. For example, on triangular billiards with corners of less than 100 degrees, it is known that there are always periodic paths—paths that the ball can follow and that return on themselves.
This can be proven mathematically. Now, change one of the corners to a slightly bigger angle, and no mathematician knows the answer anymore.
Idealized games of billiards are not just a favorite pastime of mathematicians. They also have a profound impact on physics and other sciences. Many of the questions about billiards can be phrased as questions about chaos: Do similar initial conditions of a dynamical system—whether it is a ball on a billiard table, a molecule in a gas or a bird in a flock—always lead to similar final results?
A new rule
In research carried out at the University of Amsterdam, a team of physicists has realized that by slightly changing the rules of the billiards game, the number of applications in the real world increases even further.
Mazi Jalaal, co-author of the publication and head of the group in which the research was done, explains, "In nature, many living organisms have an external form of memory. For example, they leave traces to remember where they have been. They can then use that information to either follow the same route again, or—say, when searching for food—to not explore that same region again."
The latter option led the researchers to an interesting idea: What if we add one rule to the billiards game, namely that the ball may never cross its own previous path? The result is that the effective size of the billiard table gets smaller and smaller. In fact, the ball eventually gets trapped by its own trajectory.
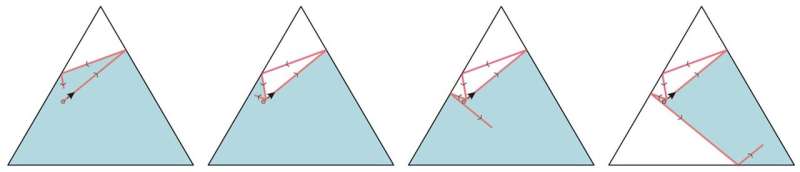
Intriguing new questions
The trapping effect makes the system even more intriguing. Even simple questions now become extremely fascinating. How far does a ball travel before it gets trapped? The answer varies, both on the shape of the table and on the starting point and direction of the ball.
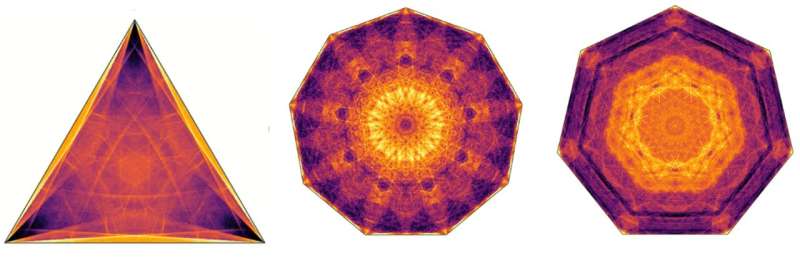
Sometimes the ball travels a length that is only a few times the size of the table, sometimes it can go for 100 times that length before it gets trapped. Where the ball eventually ends up in its trapped state is also an intricate question; repeating the experiment on a computer millions of times, every time with a slightly different starting position and velocity, leads to beautiful patterns of final configurations.
The image at the top of this text shows some of these beautiful examples. Interestingly, the resulting dynamical systems can be chaotic. Changing the starting position or velocity of the self-avoiding ball only slightly can lead to it being trapped at a completely different point on the billiard.
Additionally, contrary to what happens on an ordinary billiard table, the self-avoiding ball is not equally likely to end up just anywhere. Some regions are more likely than others. To explain and prove all of these features, the mathematicians certainly have their work cut out.
Endless applications
An interesting particularity of the publication is that both of its first authors are master students. Jalaal adds, "The idea of a 'billiard with memory' is simple enough and new enough that studying it does not require years of experience. Thijs and Stijn did a great job in making the material their own and finding clever ways to study all these new open problems. I am very happy that they can already be lead authors of a publication."
The results are only the first steps in what could be an entire new area of research. Not only are there many interesting mathematical questions that are now waiting to be answered; the applications in physics, including biophysics, are also endless.
Jalaal says, "The concept of trapping is one that begs to be explored, also in real-life systems. For instance, we know that single-celled slime molds use self-avoiding paths. Do they also get trapped, and what happens when they do? Or do they have clever mechanisms to avoid this from happening at all? Do they use it to enhance search strategies for food?
"The results would help us to better understand these biological systems, and perhaps even incorporate the lessons we learn to optimize this form of billiards with memory for use in robots."
More information: Thijs Albers et al, Billiards with Spatial Memory, Physical Review Letters (2024). DOI: 10.1103/PhysRevLett.132.157101. On arXiv: DOI: 10.48550/arxiv.2307.01734
Journal information: Physical Review Letters , arXiv
Provided by University of Amsterdam