Verifying the mathematics behind ocean modeling

Global climate models, such as the Energy Exascale Earth System Model developed by the U.S. Department of Energy, rely on many underlying equations that simulate Earth's natural processes. These include the water cycle, carbon dioxide uptake by land and water, and rates of ice melt.

Verifying and validating these equations are crucial for instilling confidence in climate models. Though some discrepancy between model predictions and actual observations is inevitable, the aim is for specific configurations of the model to converge to the correct solution at the rate scientists expect.

Continuous mathematical models must undergo a process called discretization, which converts them into forms that can be numerically solved by computers. Test cases can help with overall verification of a model by extracting subsets of the discretized equations and verifying each term.

Measuring the rate at which the numerical solutions of these test cases converge toward the exact solutions (meaning the errors approach zero) is the gold standard method for model verification. Convergence rates aligning with theoretical expectations is the best guarantee that the discretized equations are coded correctly.

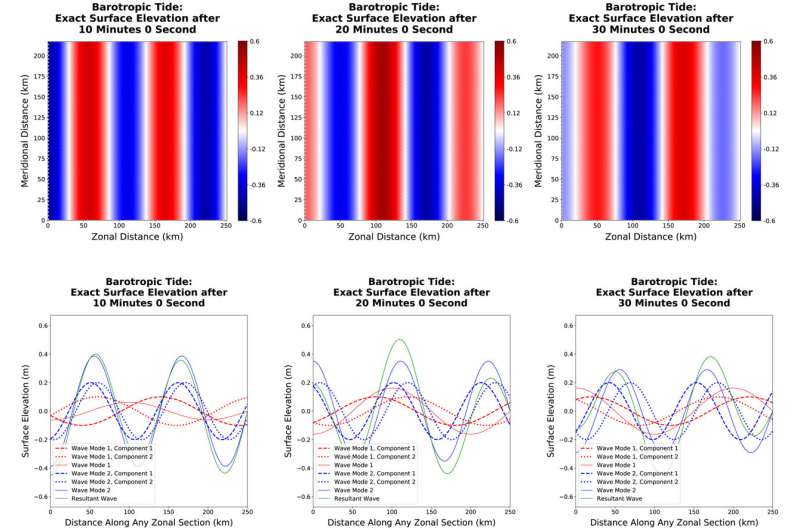
For computational efficiency, ocean models typically split their governing equations into a 3D baroclinic component that models slow internal gravity waves and ocean currents and a 2D barotropic component that models fast surface gravity waves. The barotropic component assumes the form of shallow-water equations. Siddhartha Bishnu and colleagues present a collection of test cases focused on these equations. The research is published in the Journal of Advances in Modeling Earth Systems.

To develop the test cases, the researchers drew on their experience developing the Model for Prediction Across Scales–Ocean (MPAS–Ocean), which is used to simulate ocean activity and study how it is affected by anthropogenic climate change. The authors note that their test cases are meant to verify the accuracy of the model (to ensure the discretized model equations are implemented correctly), rather than to validate the results (to ensure the model predictions resemble real-world observations).

The researchers reviewed the theoretical foundations of the shallow-water equations alongside the discretization methods, offered an overview of the test cases to ensure reproducibility, and demonstrated that the convergence rates match the anticipated predictions.

These test cases will enable other researchers to assess their models' components without the need for excessive computational power, the authors write. In addition, the test cases could be useful for broader fluid dynamics problems and serve as instructional tools for studying and developing ocean models.

This story is republished courtesy of Eos, hosted by the American Geophysical Union. Read the original story here.