The way a sperm tail moves can be explained by mathematics worked out by Alan Turing

Alan Turing might be best know for his work helping to crack Germany's "Enigma" communications code during the second world war. But he also came up with a theory where patterns can form just through chemical compounds spreading out (diffusing) and reacting with one another. This became known as reaction-diffusion theory for pattern formation.

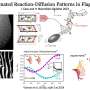
Ph.D. student James Cass and I recently published a study in Nature Communications that revealed the tail of a sperm, known as a flagellum, generates patterns as it moves—and that these patterns can be described by Turing's theory.

Patterns formed by chemical interactions create a large variety of shapes and colors such as spirals, stripes and spots. They are everywhere in nature, and are believed to be behind animal markings such as those on zebras and leopards, the whorl of seeds in a sunflower head and patterns formed by beach sand.

Turing's theory can be applied to various fields in science, from biology and robotics to astrophysics.

We wanted to explore whether there was a mathematical connection between these chemical patterns and how sperm tails move. If there was, it might suggest that nature uses similar templates to create patterns of motion at tiny scales.

Tale of a tail

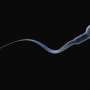
The mathematics of how the sperm flagellum moves is very complex. The flagellum uses molecular scale "motors" to effectively shape-shift. They use energy in one form and convert it into mechanical work, generating motion. These motors power tiny fibers that exist in a bundle called an axoneme. These are beautiful, geometric and slender structures that can be up to 0.05 millimeters long in human sperm—about half the width of a human hair.

The axoneme is very flexible, meaning micrometer-scale waves can travel along it. It is the active core of the flagellum and is responsible for propelling sperm cells along. They can even sense the environment around them.

The swimming motion is a result of complex interactions between passive components such as the axoneme and its elastic connector parts, active parts (the molecular motors) and the surrounding fluid.

The fluid environment in which sperm travel generates drag that resists motion by the flagellum. In order for sperm to travel, multiple, partly antagonistic, factors need to reach a balance where undulations by the flagellum propel sperm along.

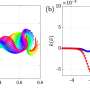
We were partially inspired by scientific findings that suggest the surrounding fluid has little effect on sperm flagellum movements. To investigate this, we created a digital "twin" of the sperm flagellum in a computer.

This twin is a representation in the computer that should behave in a very similar way to the real thing. This complex task was carried out by James F. Cass at the Polymaths Lab.

This allowed us to determine how much the surrounding fluid influenced the movement of the tail. We found that low viscosity (watery) fluids, the kind that aquatic species are adapted for, had very little effect on how the flagellum was shaped.

Using a combination of mathematical modeling, simulations and model fitting, we showed that undulations in sperm tails arise spontaneously, without the influence of their watery surroundings. This means that the flagellum has a foolproof mechanism to enable swimming in low viscosity fluids.

Mathematically, this spontaneous movement is equivalent to the way patterns arise under Turing's reaction-diffusion system that was first proposed for chemical patterns. The similarity between chemical patterns and patterns of movement was striking and unexpected.

Typically, we would not think about chemical patterns working the same way as motion patterns (or patterns of contractions), nor would we expect the mathematics to be similar. But now we know this is the case, we think the motion pattern may only need two simple ingredients. The first is chemical reactions that drive molecular motors and the second is a bending motion by the elastic flagellum. The surrounding fluid has little to no effect in aquatic environments.

The molecular motors all along the sperm's flagellum create "shearing" forces that bend the tail. If an elastic rod is bent and released, the rod will eventually unbend until it reaches a straight equilibrium. In other words, bending "diffuses" along the structure in the same way that a dye diffuses in fluid until it reaches a balanced level of dilution—known as equilibrium. It harks back to Turing's mathematics.

These findings may be used in future to better understand fertility issues associated with abnormal motion of the flagellum. The mathematics behind this could also be explored for new robotic applications, including artificial muscles and what are known as animate materials—materials that seem "alive", changing their response according to how they're being used.

The same mathematics that describes how the sperm tail moves also applies to cilia. These are thread-like projections found on many types of biological cells that propel fluid along a surface. Researching their movement could help us better understand ciliopathies, diseases caused by ineffective cilia in the human body.

However, we need to be cautious. Mathematics is an imperfect tool for examining nature's perfect work. Although this takes us a step closer to mathematically decoding spontaneous movement in flagella and cilia, the proposed animated reaction-diffusion theory is far too simple to fully capture all the complexity. Different teams have investigated whether Turing's pattern formation theory is at work in other biological systems and have found the evidence lacking.

Likewise, other mathematical models may fit equally well, or even better, with experiments. As the British statistician George Box once rightly said, "All models are wrong, but some are useful." We hope the patterns we have discovered can offer useful insights to the scientific community.

This article is republished from The Conversation under a Creative Commons license. Read the original article.