What do a jellyfish, a cat, a snake, and an astronaut have in common? Math.

Across the animal kingdom there are creatures that move through their environments not by walking or running or climbing but instead by simply changing the shape of their bodies. This kind of locomotion is found in snakes as they slither, in stingrays as they swim, and even in cats as they twist themselves to land on their feet as they fall.

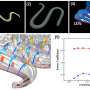
The contortions of a falling cat and a sidewinding snake might not appear to have much in common, but a team of researchers led by Caltech's Peter Schröder say they have discovered a single algorithm that describes both kinds of motion and the motions of many other animals that get around simply by changing shape.

A paper describing their work has been published in the August issue of ACM Transactions on Graphics and is being presented at this year's SIGGRAPH (Special Interest Group on Computer Graphics and Interactive Techniques) conference, which is being held August 6–10 at the Los Angeles Convention Center.

"You have all kinds of creatures who have in common that they move about by changing their shape," says Schröder, the Shaler Arthur Hanisch Professor of Computer Science and Applied and Computational Mathematics. "One classic example is a single-cell organism. How does it move? It doesn't have legs. It doesn't have wings to fly with. The only thing it can really do is change its shape.

"Once you understand that basic observation, you see there are all kinds of creatures who move by changing their shape. A snake makes an undulating motion and yet manages to move forward. Astronauts can turn in zero gravity by doing a dance-like motion that manages to turn them without the need to push off of a surface."

Schröder says all of these types of motion can be explained by the principle of least dissipation, a concept positing that natural systems will always try to be as efficient as possible. As an example, he cites an ice skate, which can easily slide forward or backward on ice but which has a great deal of difficulty sliding side to side.

If a person is wearing ice skates and wants to skate forward, they push their skates sideways away from the center line of their body. Since it's difficult for a skate to skid sideways, the skates (and the person wearing them) will move forward, since forward motion is easier and more efficient. The system consisting of the skater, the skates, and the ice favors forward motion because it wastes the least energy.

The same principle is at work when a snake undulates its way across the sandy ground of a desert. A snake, being long and skinny, can slide forward and backward much more easily than it can slide sideways. Since that undulation causes its body to slide sideways in a back-and-forth motion, much energy would be lost due to friction—unless the snake is moving forward while undulating. Since motion along the length of the snake encounters less friction, the system favors it, and the snake slithers along its merry, scaly way.

All these kinds of locomotion were modeled on computers using the principle of least dissipation as a starting point. The animals were rendered as sets of flexible nodes connected by rigid bars and allowed the researchers to examine how the creatures move in a simulated space and compare it with real life data.

Guided by the principle of least dissipation (and other math), these animal models showed movement remarkably like that seen in their real-world counterparts.

"It's just beautiful that you can identify a fairly simple governing principle of a whole class of different kinds of motion," Schröder says. "It's not 100% accurate, but shows remarkable agreement with motion observed in real life, suggesting that it captures a major part of what happens in nature.

"There's a certain mathematical beauty when you have a very simple principle that can explain a whole bunch of things at once. That's what gets me up in the morning."

The paper describing the research is titled "Motion from Shape Change." Additional co-authors Yousuf Soliman, graduate student in applied and computational math; and Oliver Gross, Marcel Padilla, Felix Knöppel, and Ulrich Pinkall of the Technical University of Berlin.