Novel mathematical technique enables better modeling of 'multiphase' fluids
Researchers have developed a mathematical technique that radically reduces the enormous computational costs of trying to model fluids that combine both liquid and gas phases, especially within rocket engines. The computational burdens of this sort of modeling have long challenged researchers to accurately describe how shockwaves in such multiphase fluids produce wear and tear in machinery.
The technique is described in a paper that appeared in the Journal of Computational Physics.
Calculations for fluid mechanics—the branch of physics concerned with the motion of liquids, gases, and anything else that acts like a fluid—can run into a computational challenge when considering the flow of materials in more than one phase or state of matter, such as a water and a gas flowing together simultaneously.
This sort of flow, termed "multiphase flow," which also covers the flow of two different liquids such as oil and water, is extremely widespread. It happens anywhere there might be a breakup of liquid droplets, and their phase changes evaporation, boiling, condensation and cavitation (the forming of small vapor-filled cavities within a liquid, i.e., bubbles).
In the oil and gas industry, for example a well is the source of a flow not just of petroleum but also natural gas and water. The flow inside a rocket engine that uses a liquid oxygen is another example of a multiphase flow, again of gaseous and liquid phases, where some of the liquid oxygen evaporates and then together with the liquid remainder is set alight in a combustion chamber.
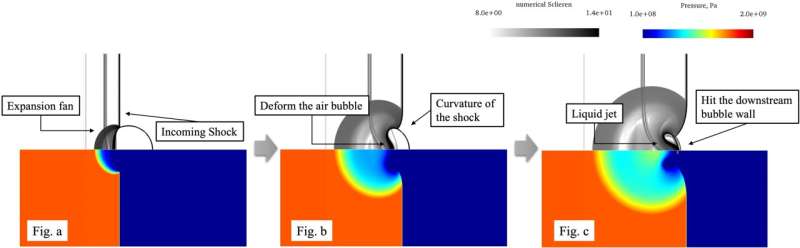
Study of multiphase flow is vital within such industries not least for how machine wear and tear occur. When the bubble vapor cavities of the earlier mentioned phenomenon of cavitation confront higher pressures, these bubbles can collapse. That collapse in turn produces a shock wave that can weather and damage machines or infrastructure.
Modeling of this is thus extremely important to industrial activities throughout much of the modern world. It is straightforward enough modeling a fluid in a single phase, but few fluids in the real world ever remain just one phase. The computational challenge here comes from quantifying the distribution of velocities of the different phases, including how velocities change at the interface between the two (or more) phases.
There are two main ways of modeling multiphase flows, the Euler-Lagrange method and the Euler-Euler method. Both are extremely computationally expensive, and both have certain drawbacks. In the Eulerian-Lagrange approach, for example, the liquid phase is expressed as a collection of particles, and, as a result, gas-liquid interfaces and primary atomization (the process of change from a bulk liquid to droplets) cannot be analyzed.
It was not until the 1990s, that increases in computing power permitted more realistic modeling of multiphase flow. Researchers for the first time were able to move up from simplified one-dimensional representations of multiphase flow to more realistic three-dimensional models.
But even with such computing power advances, multiphase model work remains computationally expensive (which means, in some really tricky cases, financially expensive too). This is especially problematic for the high degree of multiphase-flow complexity within rocket engines. The multiphase liquid and gaseous oxygen fuel combustion can be accompanied by instabilities such as resonance or chugging in the engine from fluctuations in the rate of heat release.
To address such problems, multiphase flow modeling is required that involves mathematical solutions describing both sound waves and compressible flows (in other words involving cavitation). In rocket engine research, compressible multiphase flow computation—and how to reduce its computational cost—has increasingly become an important topic of research.
Conventional methods of modeling compressible multiphase flow call for the use of a computationally expensive "exact Riemann solver" to describe interactions between air bubbles and water shockwaves (at the interface between liquid and gas phases).
"An exact Riemann solver is a method of approximation in computational fluid dynamics to describe the flux across such discontinuities," said Junya Aono, a computational fluid dynamicist with the Department of Mechanical Engineering and Material Science at Yokohama National University (YNU). "But it incurs high computation costs and also struggles with what's called the carbuncle problem in which the captured shock waves are distorted, potentially affecting heat transfer to the chamber containing the multiphase flow."
So the researchers developed a way to model compressible multiphase flow that no longer needs Riemann solvers.
"This involves a tweaking of the Simple Low-dissipation Advection Upstream Splitting Method," said Keiichi Kitamura, co-author of the paper and who is also with YNU. "This is a mathematical technique used elsewhere but can be extended to complex physical interactions, such as multiphase flows."
The tweaking—which involves careful design to take into account numerical dissipation, or the way that a simulated fluid can exhibit higher rate of diffusion that the medium does in the real world—allows accurate description of interactions of the captured shock waves and other discontinuities in multiphase flows. Crucially, all of this can be easily coded.
Any potential users of the technique can now easily produce compressible multiphase flow simulations without huge computational burdens or having to take special care in selecting the parameters for the model.
The researchers now want to apply their mathematical technique to practical 3D compressible multi-phase flow simulations, in particular with respect to rocket engines.
More information: Junya Aono et al, An appropriate numerical dissipation for SLAU2 towards shock-stable compressible multiphase flow simulations, Journal of Computational Physics (2022). DOI: 10.1016/j.jcp.2022.111256
Provided by Yokohama National University