Insights into optical resonances determined by the topology of the Möbius strip
In the current issue of Nature Photonics, Prof. Dr. Oliver G. Schmidt, Dr. Libo Ma and partners present a strategy for observing and manipulating the optical Berry phase in Möbius ring microcavities. In their research paper, they discuss how an optical Berry phase can be generated and measured in dielectric Möbius rings. Furthermore, they present the first experimental proof of the existence of a variable Berry phase for linearly or elliptically polarized resonant light.
A Möbius strip is a fascinating object. You can easily create a Möbius strip when twisting the two ends of a strip of paper by 180 degrees and connecting them together. Upon closer inspection, you realize that this ribbon has only one surface that cannot be distinguished between inside and outside or below and above. Because of this special topological property, the Möbius strip has become an object of countless mathematical discourses, artistic representations and practical applications, for example, in paintings by M.C. Escher, as a wedding ring, or as a drive belt to wear both sides of the belt equally.
Optical ring resonators
Closed bands or rings also play an important role in optics and optoelectronics. Until now, however, they have not consisted of Möbius strips and they are not made of paper, but are made of optical materials, for example, silicon and silicon dioxide or polymers. These "normal" rings are also not centimeters in size, but micrometers. If light with a certain wavelength propagates in a micro ring, constructive interference causes optical resonances to occurs. This principle can be exemplified by a guitar string, which produces different tones at different lengths—the shorter the string, the shorter the wavelength, and the higher the tone.
An optical resonance or constructive interference occurs exactly when the circumference of the ring is a multiple of the wavelength of the light. In these cases the light resonates in the ring and the ring is called an optical ring resonator. In contrast, the light is strongly attenuated and destructive interference occurs when the circumference of the ring is an odd multiple of half the wavelength of the light. Thus, an optical ring resonator enhances light of certain wavelengths and strongly attenuates light of other wavelengths that do not "fit" in the ring. In technological terms, the ring resonator acts as an optical filter that, integrated on a photonic chip, can selectively "sort" and process light. Optical ring resonators are central elements of optical signal processing in today's data communication networks.
How polarized light circulates in the Möbius strip
Besides the wavelength, polarization is an essential property of light. Light can be polarized in various ways, for example linearly or circularly. If light propagates in an optical ring resonator, the polarization of the light does not change and remains the same at every point in the ring.
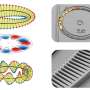
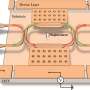
The situation changes fundamentally if the optical ring resonator is replaced by a Möbius strip or better, a Möbius ring. To better understand this case, it helps to consider the detail of the geometry of the Möbius ring. The cross-section of a Möbius ring is typically a slender rectangle in which two edges are much longer than their two adjacent edges, such as in a thin strip of paper.
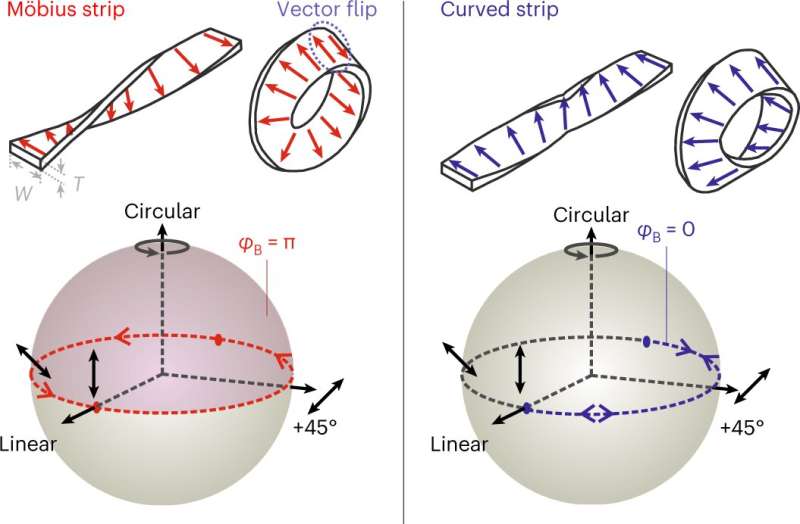
Let us now assume that linearly polarized light circulates in the Möbius ring. Because the polarization prefers to align itself in the direction of the long cross-sectional side of the Möbius ring, the polarization continuously rotates up to 180 degrees while passing completely around the Möbius ring. This is a huge difference to a "normal" ring resonator, in which the polarization of the light is always maintained.
And that's not all. The twisting of the polarization causes a change in the phase of the light wave, so that the optical resonances no longer occur at full wavelength multiples that fit into the ring, but at odd multiples of half the wavelength. Part of the research group had already predicted this effect theoretically in 2013. This prediction, in turn, is based on work by physicist Michael Berry, who introduced the eponymous "Berry phase" in 1983, describing the change in the phase of light whose polarization changes as it propagates.
First experimental evidence
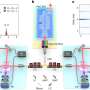
In the current article published in the journal Nature Photonics, the Berry phase of light circulating in a Möbius ring is experimentally revealed for the first time. For this purpose, two rings with the same diameter were made. The first is a "normal" ring and the second is a Möbius ring. And as predicted, the optical resonances in the Möbius ring appear at different wavelengths compared to the "normal" ring.
The experimental results, however, go much beyond previous predictions. For example, the linear polarization not only rotates, but also becomes increasingly elliptical. The resonances do not occur exactly at odd multiples of half the wavelength, but quite generally at non-integer multiples. To find out the reason for this deviation, Möbius rings with decreasing strip width were made. This study revealed that the degree of ellipticity in the polarization and the deviation of the resonance wavelength compared to the "normal" ring became progressively weaker as the Möbius strip became narrower and narrower.
This can be easily understood because the special topological properties of the Möbius ring merge into the properties of a "normal" ring when the width of the band decreases to that of its thickness. However, this also means that the Berry phase in Möbius rings can be easily controlled by simply changing the design of the band.
In addition to the fascinating new fundamental properties of optical Möbius rings, new technological applications are also opening up. The tunable optical Berry phase in Möbius rings could serve for all-optical data processing of classical bits as well as qubits and support quantum logic gates in quantum computation and simulation.
More information: Jiawei Wang et al, Experimental observation of Berry phases in optical Möbius-strip microcavities, Nature Photonics (2022). DOI: 10.1038/s41566-022-01107-7
Journal information: Nature Photonics
Provided by Chemnitz University of Technology