The mathematics that makes us realize we don't know much: Behavior of spin glasses
Spin glasses are alloys formed by noble metals in which a small amount of iron is dissolved. Although they do not exist in nature and have few applications, they have nevertheless been the focus of interest of statistical physicists for some 50 years. Studies of spin glasses were crucial for Giorgio Parisi's 2021 Nobel Prize in Physics.
The scientific interest of spin glasses lies in the fact that they are an example of a complex system whose elements interact with each other in a way that is sometimes cooperative and sometimes adversarial. The mathematics developed to understand their behavior can be applied to problems arising in a variety of disciplines, from ecology to machine learning, not to mention economics.
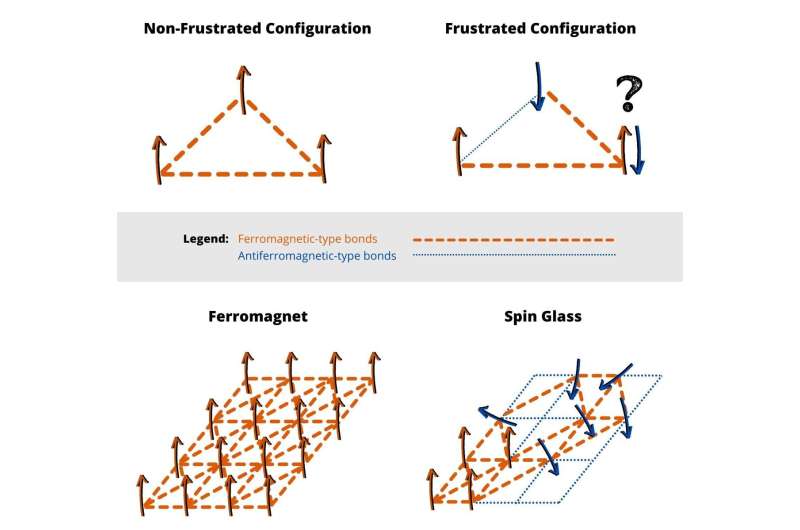
Spin glasses are magnetic systems, that is, systems in which individual elements, the spins, behave like small magnets. Their peculiarity is the co-presence of ferromagnetic-type bonds, which tend to align the spins, with antiferromagnetic-type bonds, which tend to orient them in opposite directions.
This causes lower-energy configurations to exhibit residual frustration: it is not possible to find an arrangement of spins that satisfies all bonds. The frustrated configurations are also clustered in a huge (exponential!) number of possible equilibria. This is in stark contrast to what happens in purely ferromagnetic systems, where at low temperature only two states are admissible (spin aligned "up" or spin aligned "down").
To make an analogy with an ecosystem, having a high number of equilibria indicates a resilient ecosystem, able to cope, for example, with the disappearance of a species, through a limited number of rearrangements. A low equilibrium number describes a fragile system, which requires numerous and complicated rearrangements to return to equilibrium and can, therefore, be seriously damaged, if not destroyed, by relatively small perturbations.
This phenomenology has been well elucidated and mathematically described in systems living in infinite dimension, so-called mean-field systems, the solution to which was provided by Parisi in 1979 and then better understood in subsequent years with the help of Marc Mézard (now a full professor at Bocconi) and Michelangelo Virasoro.
"One of the most debated issues," as Carlo Lucibello, Assistant Professor in the Department of Computing Sciences and co-author, with Parisi and others, of a paper just published in Physical Review Letters explains, "is to what extent mean-field phenomenology applies in low dimensionality."
For we know that in dimension 1, that is, on one spin chain, the system is always in a paramagnetic phase, so by lowering the temperature there are no transitions either to a spin glass phase with its many equilibria or to a simple ferromagnetic phase.
"There is a so-called critical upper dimension," Lucibello says, "above which the mean-field theory applies, allowing us to predict the exponents governing the transition. At the moment, however, no one can say for sure what this dimension is (5, 6, or a non-integer number?) and what happens below it."
The paper just published by Lucibello and co-authors introduces a new mathematical technique for analyzing finite-dimensional systems. The new theory predicts a critical higher dimension of 8, so we can reasonably conclude that spin glasses in our three-dimensional world are unlikely to be described by a mean-field theory and that there is still a lot of work to do in this branch of theoretical physics.
More information: Maria Chiara Angelini et al, Unexpected Upper Critical Dimension for Spin Glass Models in a Field Predicted by the Loop Expansion around the Bethe Solution at Zero Temperature, Physical Review Letters (2022). DOI: 10.1103/PhysRevLett.128.075702
Journal information: Physical Review Letters
Provided by Bocconi University