Using math proofs, experiments and simulations to show how a material wrinkles when flattened

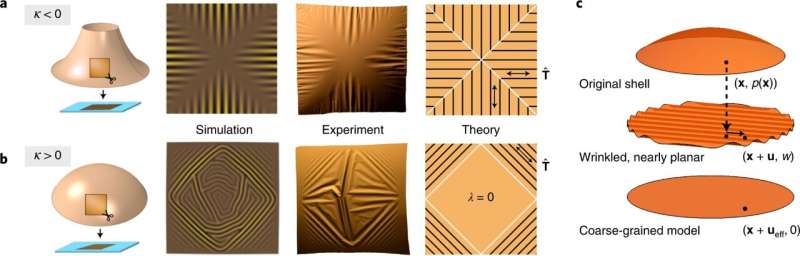
A team of researchers from the University of Illinois at Chicago, Syracuse University and the University of Pennsylvania, has developed a means for showing how a certain piece of material wrinkles after it has been flattened. In their paper published in the journal Nature Physics, the group describes experiments they conducted with tiny pieces of plastic.

Prior research has shown that it is difficult to understand the rules of wrinkling for almost any material—there are just too many variables involved to get a handle on it. In this new effort, the researchers sought to understand how wrinkling works in a single material as it wrinkles in a controllable setting.

The work followed up on work done by Ian Tabasco, a mathematician at the University of Illinois Chicago. He developed a theory centered on the energy costs involved when a material wrinkles. To test his theories, the researchers first created simulations of material responses to prodding in ways described by Tabasco's math formulas. However, they found that a simulated environment was not workable, so they set up a real-world testing scenario.

They placed thin, flat pieces of plastic on a curved glass surface and then spun it, which made the plastic even thinner as it took on the shape of the curved glass. Then, they placed the curved plastic pieces on a wet surface and watched as the water tension forced the plastic to wrinkle. They then used data from the wrinkles that developed to fine-tune the simulations and found that doing so repeatedly led to the generation of rules that described how wrinkles appeared and behaved.

The researchers found, for example, wrinkles forming in rows instead of on the edges of a patch were dependent on the shape of the piece of plastic just prior to the formation of wrinkles. They also found that they were able to predict where wrinkles would appear in a given piece of plastic if they split up the plastic area into many small subunits. Under such conditions, they found Tabasco's calculations could be used to describe the types of ripples that would appear and lead to wrinkling.

© 2022 Science X Network